9. WGAN 이론 및 구현
WGAN
WGAN, 즉 Wasserstein GAN은 전통적인 GAN(Generative Adversarial Network)의 학습 안정성 문제를 해결하기 위해 제안된 모델. WGAN의 가장 중요한 특징은 목적 함수와 판별자(discriminator)를 수정하여, 생성자(generator)와 판별자 사이의 경쟁이 더 안정적으로 이루어지도록 한 점에 있다.
WGAN의 핵심 개념
Wasserstein 거리 사용: WGAN은 전통적인 GAN의 목적 함수 대신 Wasserstein 거리(또는 Earth Mover’s 거리)를 사용. 이 거리 측정은 두 확률 분포 간의 거리를 더 잘 캡처하며, 학습 과정에서의 모드 붕괴(mode collapse) 문제와 훈련의 불안정성을 줄여준다.
판별자의 마지막 층에서 시그모이드 활성화 함수 제거: WGAN에서는 판별자의 마지막 층에서 시그모이드 활성화 함수를 제거. 판별자는 이제 확률을 출력하는 대신 실수 값을 직접 출력하는 ‘크리틱(critic)’으로 기능하며, 이 값은 입력 이미지가 실제 분포에서 얼마나 멀리 떨어져 있는지를 나타낸다. 크리틱의 목적은 실제 이미지에 대해서는 높은 값을, 생성된 이미지에 대해서는 낮은 값을 출력한다.
가중치 클리핑(Weight Clipping): WGAN에서는 판별자의 가중치를 특정 범위 내로 제한. 이는 판별자 함수가 Lipschitz 연속성 조건을 만족시키도록 하여, 학습 과정을 안정화하는 데 도움을 준다.
Wasserstein 거리 (Earth Mover’s 거리)
Wasserstein 거리는 두 확률 분포 간의 거리를 측정하는 방법으로, 한 분포의 확률 질량을 다른 분포로 “옮기는” 데 필요한 “최소 작업”을 나타낸다. 직관적으로, 하나의 분포를 다른 분포로 변환하기 위해 확률 질량을 이동시키는 데 필요한 평균 거리를 측정한다. 이는 “Earth Mover’s”라는 이름으로도 알려져 있으며, 두 분포 사이를 연결하는 가장 효율적인 방법을 찾는 것으로 생각할 수 있다.
Lipschitz 연속성
함수가 Lipschitz 연속이라는 것은 함수의 변화율이 특정 상수 $K$로 제한된다는 것을 의미한다. 즉, 모든 $x$와 $y$에 대해 다음 불등식이 성립한다.
| $ | f(x) - f(y) | \leq K | x - y | $ |
WGAN에서는 판별자(여기서는 크리틱으로 명명)가 Lipschitz 연속 함수가 되도록 강제한다. 이는 가중치 클리핑(weight clipping)이나 그래디언트 페널티(gradient penalty)와 같은 기법을 사용하여 달성할 수 있으며, 이를 통해 학습 과정이 안정화된다.
Loss 공식
WGAN의 목적 함수:
생성자의 손실 (Generator Loss): $L_G = -\mathbb{E}_{z \sim p_z(z)}[C(G(z))]$ 생성자는 생성된 이미지에 대한 크리틱의 출력을 최대화하려고 한다.
판별자(크리틱)의 손실 (Discriminator/Critic Loss): $L_D = \mathbb{E}{x \sim p{data}(x)}[C(x)] - \mathbb{E}_{z \sim p_z(z)}[C(G(z))]$ 크리틱은 실제 이미지에 대해서는 그 값을 최대화하고, 생성된 이미지에 대해서는 최소화하려고 한다.
이 공식에서 $D(x)$ 는 크리틱이 출력하는 실수 값이며, $G(z)$ 는 생성자가 잠재 공간 $z$ 에서 생성한 이미지. $p_{data}(x)$ 는 실제 데이터 분포를, $p_z(z)$ 는 잠재 공간의 분포를 나타낸다.
WGAN의 이러한 손실 함수는 생성자와 판별자 사이의 경쟁을 Wasserstein 거리의 관점에서 재정의함으로써, GAN 학습의 주요 문제점을 해결하고 결과적으로 더 안정적인 학습과 더 높은 품질의 생성 이미지를 얻을 수 있도록 한다.
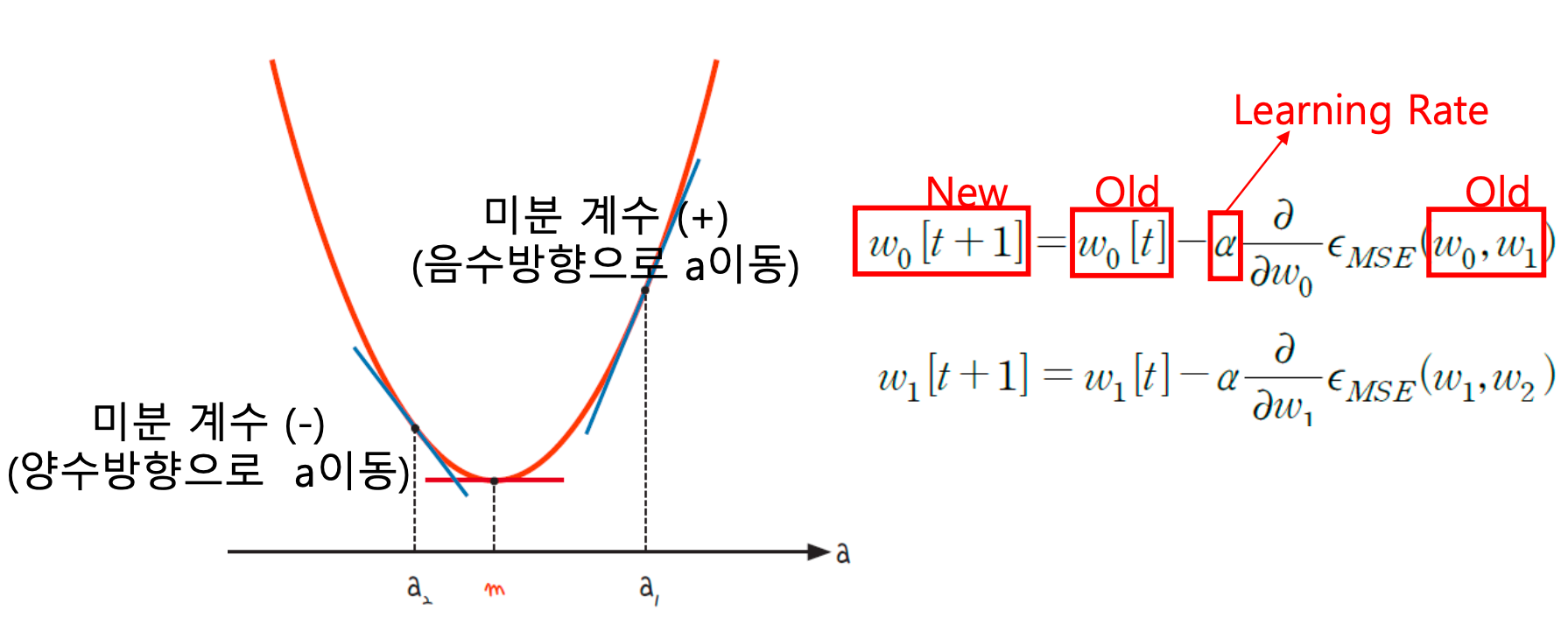
경사 하강법과 양의 손실
- 경사 하강법: 모델의 손실을 최소화하기 위해 파라미터를 업데이트하는 과정. 손실 함수가 양수일 때, 이 값을 감소시키기 위해 경사 하강법을 사용. 즉, 손실 함수의 그래디언트(기울기)의 반대 방향으로 파라미터를 조정.
경사 상승법과 음의 손실
생성자 손실과 음수 부호: WGAN에서 생성자의 손실 함수에 음수 부호를 붙이면, 손실 값이 음수가 된다. 이 경우, 손실 값을 “감소”시키는 것이 아니라, 사실상 그 절대값을 “증가”시키는 방향으로 최적화를 진행해야 한다. 이는 경사 상승법(Gradient Ascent)의 개념과 일치한다.
경사 상승법의 적용: 손실 함수의 값이 음수일 때, 이 음수 값을 더 큰 음수로 만들기 위해서는 손실 함수의 최대화를 추구해야 한다. 이는 손실 함수의 그래디언트 방향으로 파라미터를 조정하는 것을 의미하며, 이 과정을 경사 상승법이라고 한다. 생성자는 크리틱으로부터 높은 평가(점수)를 받기 위해, 즉 손실 함수(음수 부호가 적용된)의 절대값을 증가시키는 방향으로 최적화를 진행한다.
따라서, WGAN에서 생성자의 최적화 과정을 이해할 때, 손실 함수에 음수 부호를 붙여서 사용하는 것은 최적화의 방향을 경사 상승법으로 전환하는 효과를 가진다. 이는 생성자가 크리틱으로부터의 평가를 최대화하려는 목적을 달성하기 위한 수학적인 표현 방법. 생성자는 이 과정에서 손실 함수의 음수 값을 더 큰 음수로 만드는 방향, 즉 크리틱의 평가를 최대화하는 방향으로 파라미터를 업데이트하게 된다.
WGAN 구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import argparse
import os
import numpy as np
import math
import cv2
import matplotlib.pyplot as plt
import torchvision.transforms as transforms
from torchvision.utils import save_image
from torch.utils.data import DataLoader
from torchvision import datasets
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F
import torch
os.makedirs("images", exist_ok=True)
def weights_init_normal(m):
classname = m.__class__.__name__
if classname.find("Conv") != -1:
torch.nn.init.normal_(m.weight.data, 0.0, 0.02)
elif classname.find("BatchNorm") != -1:
torch.nn.init.normal_(m.weight.data, 1.0, 0.02)
torch.nn.init.constant_(m.bias.data, 0.0)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Option():
n_epochs = 200 # 학습을 반복 에폭 수
batch_size = 64 # 한 번에 학습할 데이터의 수
lr = 0.00005 # 학습률
n_cpu = 8 # 배치 생성 시 사용할 CPU 스레드 수
latent_dim = 100 # 잠재 공간의 차원 수
n_critic = 5 # critic의 수
img_size = 28 # 이미지의 각 차원의 크기
channels = 1 # 이미지 채널의 수
clip_value = 0.01 # 판별자 가중치의 최소 및 최대 클립 값
sample_interval = 500 # 이미지 샘플링 간격
opt = Option()
# CUDA가 사용 가능한 경우 사용하도록 설정
cuda = True if torch.cuda.is_available() else False
# 이미지의 모양을 설정합니다. (채널 수, 이미지 너비, 이미지 높이)의 형태로 설정됩니다.
img_shape = (opt.channels, opt.img_size, opt.img_size)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
import numpy as np
import torch
import torch.nn as nn
class Generator(nn.Module):
def __init__(self):
super(Generator, self).__init__()
# 생성자의 뉴럴 네트워크 블록을 정의합니다.
def block(in_feat, out_feat, normalize=True):
layers = [nn.Linear(in_feat, out_feat)] # 선형 레이어
if normalize: # normalize가 True인 경우 배치 정규화를 적용합니다.
layers.append(nn.BatchNorm1d(out_feat, 0.8))
layers.append(nn.LeakyReLU(0.2, inplace=True)) # LeakyReLU 활성화 함수
return layers
# 정의된 블록을 순차적으로 적용하여 생성자 모델을 구축합니다.
self.model = nn.Sequential(
*block(opt.latent_dim, 128, normalize=False), # 첫 번째 블록, 배치 정규화 없음
*block(128, 256), # 차원을 128에서 256으로 증가
*block(256, 512), # 차원을 256에서 512로 증가
*block(512, 1024), # 차원을 512에서 1024로 증가
nn.Linear(1024, int(np.prod(img_shape))), # 이미지 형태에 맞게 최종 차원 매핑을 위한 선형 레이어
nn.Tanh() # 출력을 [-1, 1] 범위로 조정하기 위한 Tanh 활성화 함수
)
def forward(self, z):
img = self.model(z) # 잠재 벡터 z로부터 이미지 생성
# 출력을 이미지 차원으로 재구성합니다. 예: [batch_size, channels, img_size, img_size]
img = img.view(img.shape[0], *img_shape)
return img # 생성된 이미지 반환
class Discriminator(nn.Module):
def __init__(self):
super(Discriminator, self).__init__()
# 선형 레이어와 LeakyReLU 활성화 함수를 사용하여 판별자 모델을 구성합니다.
self.model = nn.Sequential(
nn.Linear(int(np.prod(img_shape)), 512), # 이미지를 평탄화하고 모델에 입력
nn.LeakyReLU(0.2, inplace=True), # 첫 번째 LeakyReLU 활성화
nn.Linear(512, 256), # 차원을 512에서 256으로 축소
nn.LeakyReLU(0.2, inplace=True), # 두 번째 LeakyReLU 활성화
nn.Linear(256, 1), # 단일 값(스칼라) 출력을 위한 최종 레이어
# 주의: 여기서는 시그모이드 활성화 함수를 사용하지 않습니다. WGAN은 확률을 출력하지 않습니다.
)
def forward(self, img):
img_flat = img.view(img.shape[0], -1) # 입력 이미지를 평탄화
validity = self.model(img_flat) # 평탄화된 이미지를 모델에 전달
return validity # 판별자의 판단(진짜 또는 가짜) 반환
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# Generator와 Discriminator 클래스의 인스턴스를 생성
generator = Generator()
discriminator = Discriminator()
# CUDA를 사용할 수 있는 경우, 모델을 GPU 메모리로 이동
if cuda:
generator.cuda()
discriminator.cuda()
# MNIST 데이터셋을 로드하고, 배치 단위로 데이터를 제공하는 DataLoader를 생성
os.makedirs("dataset/mnist", exist_ok=True)
dataloader = torch.utils.data.DataLoader(
datasets.MNIST(
"dataset/mnist",
train=True,
download=False,
transform=transforms.Compose([transforms.ToTensor(), transforms.Normalize([0.5], [0.5])]),
),
batch_size=opt.batch_size,
shuffle=True,
)
# RMSprop 최적화기를 사용하여 각 모델의 파라미터를 업데이트. 학습률은 옵션에서 설정한 값을 사용.
optimizer_G = torch.optim.RMSprop(generator.parameters(), lr=opt.lr)
optimizer_D = torch.optim.RMSprop(discriminator.parameters(), lr=opt.lr)
# cuda를 사용할 수 있는 경우 Tensor를 GPU에, 그렇지 않으면 CPU에 할당.
# 이 Tensor는 후에 잠재 공간 벡터를 생성하거나 real/fake 레이블을 생성하는 데 사용.
Tensor = torch.cuda.FloatTensor if cuda else torch.FloatTensor
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
# 처리한 배치 수를 카운트하는 변수를 0으로 초기화합니다.
batches_done = 0
# 설정한 에폭 수만큼 학습을 반복합니다.
for epoch in range(opt.n_epochs):
# DataLoader는 배치 단위로 데이터를 제공합니다. 각 배치에 대해 학습을 반복합니다.
for i, (imgs, _) in enumerate(dataloader):
# 실제 이미지를 GPU에 올리고 Variable로 감싼다.
"""
1. 입력 구성: 실제 이미지 `real_imgs`를 네트워크에 적합한 형태로 변환.
`Variable`과 `Tensor` 변환을 사용하여 데이터를 처리
"""
real_imgs = Variable(imgs.type(Tensor))
# ---------------------
# Train Discriminator
# ---------------------
# 판별자의 그래디언트를 초기화
optimizer_D.zero_grad()
# 생성자 입력으로 사용할 잠재 벡터 `z`를 정규 분포에서 샘플
z = Variable(Tensor(np.random.normal(0, 1, (imgs.shape[0], opt.latent_dim))))
# 샘플링한 벡터를 사용해 생성자가 가짜 이미지 생성
fake_imgs = generator(z).detach()
# 판별자의 손실을 계산합니다. 이 손실은 판별자가 실제 이미지와 생성된 이미지를 얼마나 잘 구별하는지를 측정
# 이 손실은 판별자가 실제 이미지를 더 높은 값으로, 가짜 이미지를 더 낮은 값으로 평가하도록 유도.
"""
torch.mean(discriminator(fake_imgs))
D에게 이건 가짜 라고 알려줘야 함 즉 작은 값(loss라 하면 헷갈리니 point라 함)을 내뱉어야함
그러니 그라디언트의 반대 방향으로 움직이는게 맞음
-torch.mean(discriminator(real_imgs))
D에게 이건 진짜임을 알려줘야함 즉 큰 값을 내뱉어야 함 그러니 그라디언트 방향으로 움직여야 큰 값(point)이 나옴
"""
point_D = -torch.mean(discriminator(real_imgs)) + torch.mean(discriminator(fake_imgs))
# 판별자의 그래디언트를 계산하고, 그래디언트를 사용해 판별자의 파라미터를 업데이트.
point_D.backward()
optimizer_D.step()
# 판별자의 가중치를 클리핑. 이는 WGAN에서 경험적으로 안정성을 높이는 방법
"""
WGAN에서는 판별자의 가중치를 특정 범위 내로 제한. 이는 판별자 함수가 Lipschitz 연속성을 만족하도록 하는데 중요하다.
p.data.clamp_(-opt.clip_value, opt.clip_value) 를 사용하여 각 파라미터 `p`를
`-opt.clip_value`와 `opt.clip_value` 사이로 제한
"""
for p in discriminator.parameters():
p.data.clamp_(-opt.clip_value, opt.clip_value)
# n_critic번 마다 생성자를 학습.
if i % opt.n_critic == 0:
# -----------------
# Train Generator
# -----------------
# 생성자의 그래디언트를 초기화.
optimizer_G.zero_grad()
# 샘플링한 벡터를 사용해 생성자가 이미지를 생성하게 한다.
gen_imgs = generator(z)
# 생성자의 손실을 계산. 이 손실은 생성자가 판별자를 얼마나 잘 속였는지를 측정.
"""
-torch.mean(discriminator(gen_imgs)) G는 큰 값이 나오길 원함 그럼 그라디언트 방향으로 움직여야 큰 값이 나옴
"""
point_G = -torch.mean(discriminator(gen_imgs))
# 생성자의 그래디언트를 계산하고, 그래디언트를 사용해 생성자의 파라미터를 업데이트.
point_G.backward()
optimizer_G.step()
# 현재까지 처리한 배치의 수를 계산
batches_done = epoch * len(dataloader) + i
# 일정 간격으로 로그를 출력하고, 생성된 이미지를 저장
if batches_done % opt.sample_interval == 0:
print(
"[Epoch %d/%d] [Batch %d/%d] [D loss: %f] [G loss: %f]" %
(epoch, opt.n_epochs, batches_done % len(dataloader), len(dataloader),
point_D.item(), point_G.item())
)
save_image(gen_imgs.data[:25], "images/%d.png" % batches_done, nrow=5, normalize=True)
# 생성된 이미지를 출력
plt.figure(figsize = (5,5))
img1 = cv2.imread("images/%d.png" %batches_done)
plt.imshow(img1, interpolation='nearest')
plt.axis('off')
plt.show()
- Discriminator 학습:
torch.mean(discriminator(fake_imgs))에서, Discriminator는 가짜 이미지를 가짜로 잘 인식하도록 해야 하므로, 이 항의 값을 최소화하려고 한다. 즉, 가짜 이미지에 대한 Discriminator의 출력이 낮아야 한다. 이를 위해, 이 항의 기울기(그라디언트)에 반대 방향으로 학습을 진행한다.-torch.mean(discriminator(real_imgs))에서는, Discriminator가 실제 이미지를 진짜로 잘 인식하도록 해야 하므로, 이 항의 값을 최대화하려고 한다. 이는 실제 이미지에 대한 Discriminator의 출력이 높아야 함을 의미하므로, 이 항의 기울기 방향으로 학습을 진행한다.
- Generator 학습:
point_G = -torch.mean(discriminator(gen_imgs))에서, Generator는 생성된 가짜 이미지가 진짜로 잘 판별되기를 원한다. 즉, Discriminator가 생성된 이미지를 진짜로 판별하도록 만들어야 한다. 이를 위해, 이 항의 값을 최대화하려고 합니다. 따라서, 이 항의 기울기 방향으로 학습을 진행한다.
“그라디언트 방향으로 움직인다”는 것은 해당 변수의 손실을 줄이기 위해 기울기(손실 함수의 미분값)가 가리키는 방향으로 변수 값을 업데이트한다는 의미이다. 반면, “그라디언트의 반대 방향으로 움직인다”는 것은 손실을 증가시키기 위해, 또는 최소화 과정에서 부호를 반전시켜 기울기의 반대 방향으로 변수 값을 업데이트한다는 의미이다. 이는 경사 하강법(Gradient Descent)과 경사 상승법(Gradient Ascent)의 기본 원리에 근거한다.