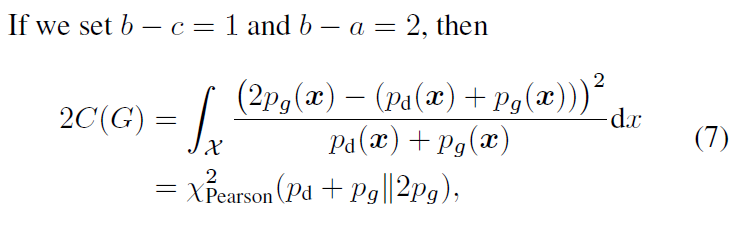8. LSGAN 이론 및 구현
Least Squares Generative Adversarial Network 이론
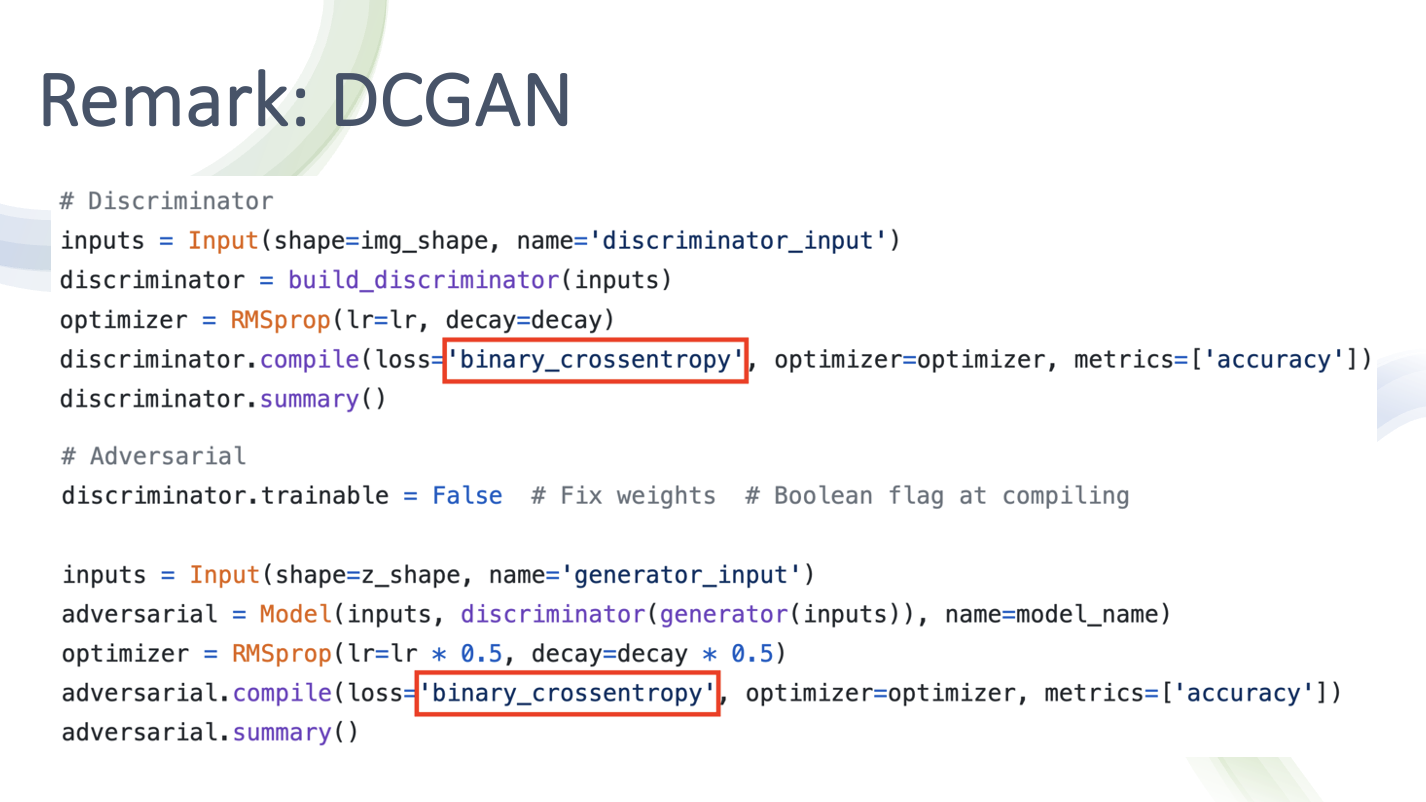
- 손실함수로 바이너리 크로스 엔트로피 로스를 사용
- 바이너리 크로스 엔트로피를 사용해 minmax게임을 풀었다
- 바이너리 크로스 엔트로피 로스는 입력에 대한 예측의 유사도
- (얼마나 진짜와 유사한가, 유사할수 있도록 얼마를 조절하면 되는가 에 대한 정보)
- 코드상에서 바이너리 크로스 엔트로피라 명시
- Discriminator와 Adversarial (G가 노이즈를 받아 G에서 나온 출력을 D가 받는 일련의 과정을 묶은 것) 둘 다 바이너리 크로스 엔트로피로 손실을 측정한 후 Optimization을 수행(Gradient를 최적화 한다)
- LSGAN은 바이너리 크로스 엔트로피를 사용하는 것이 아닌 Least Square를 사용
- 기존 GAN에서 Sigmoid cross entropy loss(= binary cross entropy loss) 를 사용
- 입력에 대해 예측을 수행했을 때 얼마나 진짜와 비슷한가
- 그런데 이 BCE를 사용하면 Gradient vanishing문제 발생
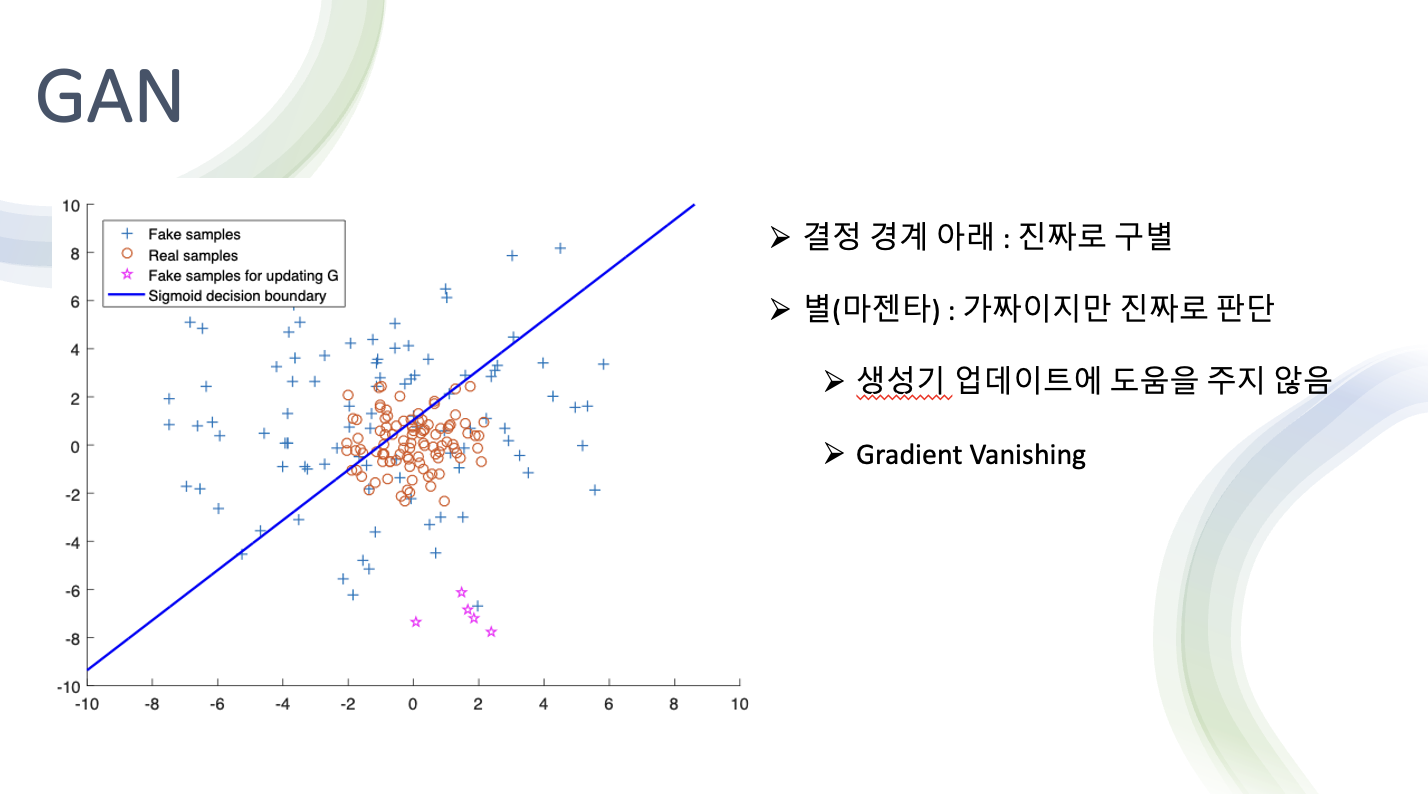
- 위 그래프가 BCE Error를 썼을 때 양상
- 빨간 동그라미가 진짜 데이터 분포
파란색 + 가 G가 만들어낸 Fake sample들
- 마젠타 : fake sample인데 결정경계를 기준으로 아래가 진짜 위가 가짜로 판단
- D입장에서는 마젠타 색상이 결정경계 아래에 있기 때문에 가짜지만 진짜라고 판단
- 즉 이미 진짜라고 판단 했기 때문에 G 업데이트에 도움을 주지 않는다
- 하지만 실제로는 Real 과 가깝게 이동을 할 필요가 있음
- 이런 필요가 있음에도 불구하고 업데이트에 이미 진짜로 판단 중이기 때문에 도움을 주지 않는다 (Gradient Vanishing)
- LSGAN의 해결법
- 손실함수를 Least square로 바꿈
- MSE와 비슷하게 실제와 가짜의 차이를 거리로 측정
- 이 방법으로 가짜 데이터의 거리를 측정 하고 그 거리를 낮추는 방향으로 학습
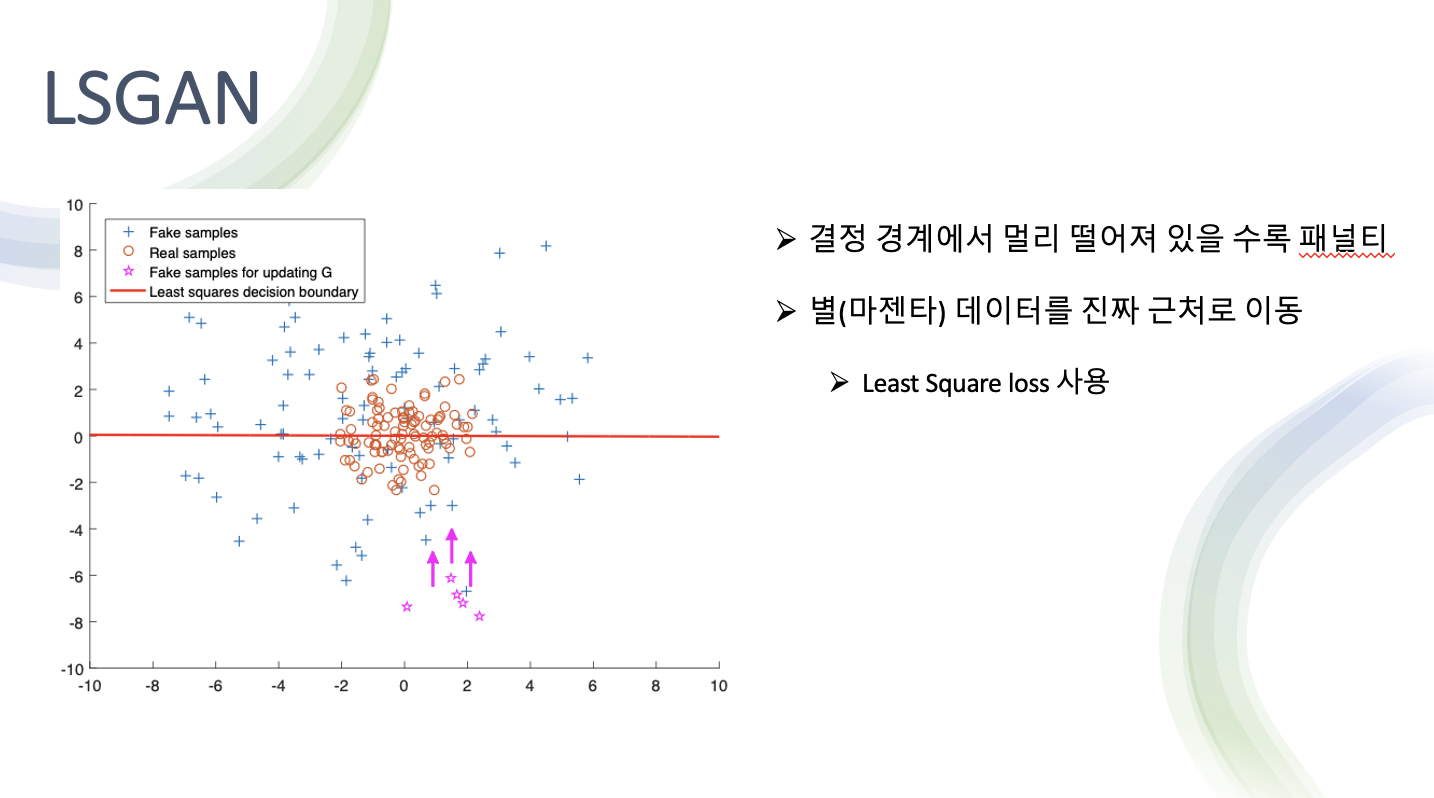
- 설명을 그림으로 나타낸 것
- 빨간색 선이 결정경계
- 가짜 데이터가 멀리 떨어져 있을 수록 패널티 부여
- 손실함수는 이 패널티를 줄이기 위해 결정경계에 가깝게 데이터를 이동
- 결국 real data분포에 더 가깝게 fake data 생성
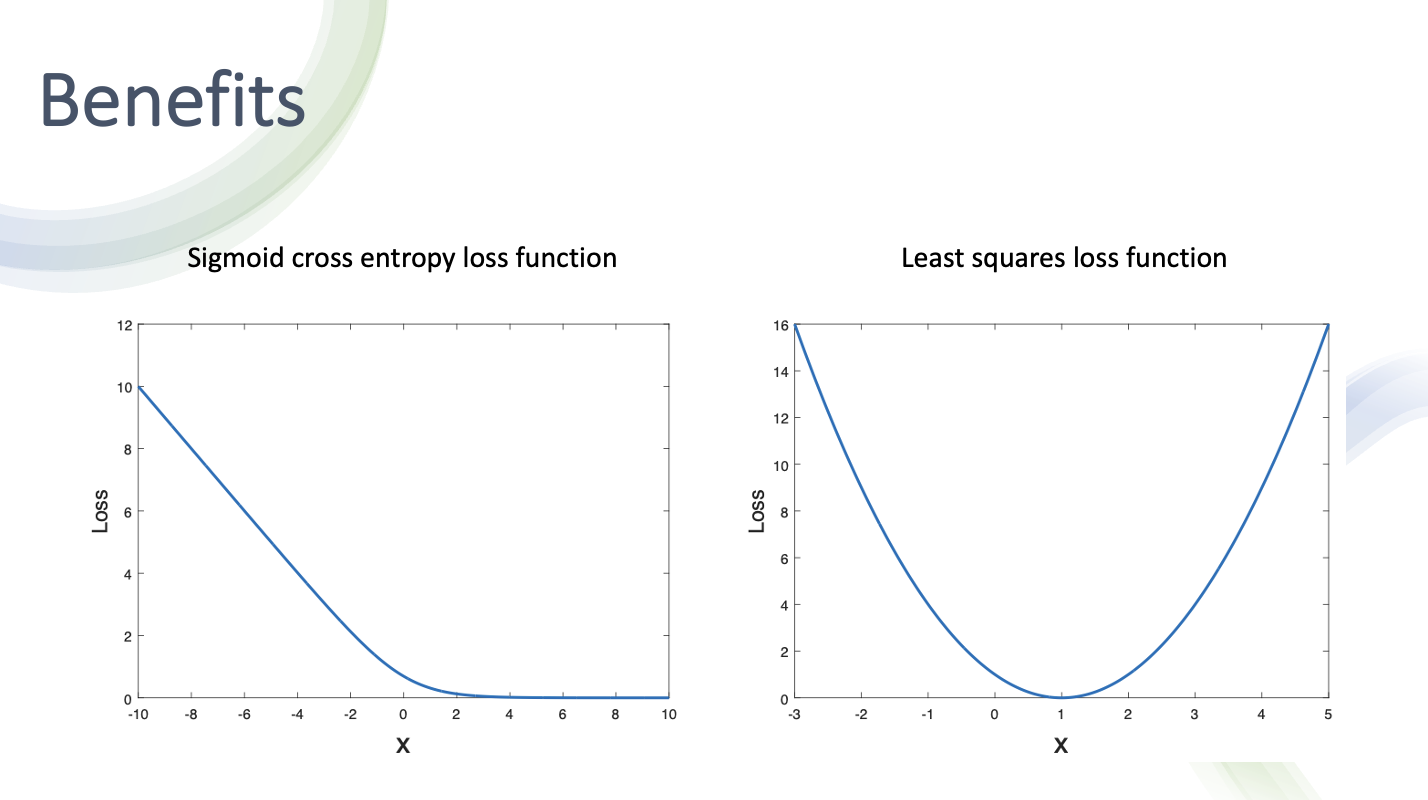
- sigmoid cross entropy loss funciton과 least squares loss function 비교
- sigmoid cross entropy loss funciton은 어느 시점 이상으로 가게되면 0이 되어 버림
- 반면 least squares loss function는 딱 한점에서만 0이고 전부 Loss값 존재 그래서 최적화 할 때 한점으로 수렴할 수 있어서 안정적으로 학습할 수 있다
- 식으로 보면 기존의 GAN은 위 식으로 minmax게임을 해결
- LSGAN은 약간 거리라는 개념이 들어가도록 변경해서 해결
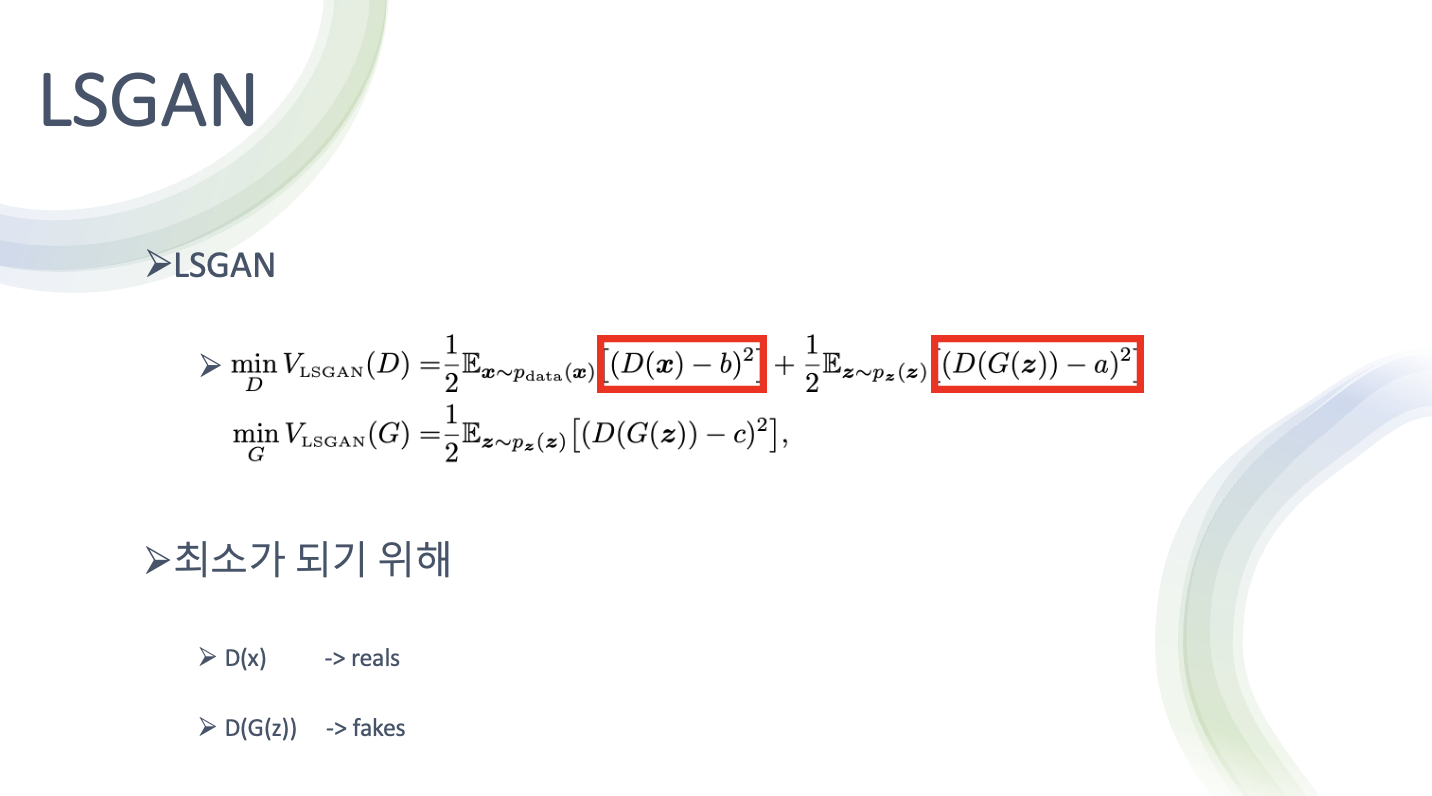
- a 가 fake label
b 가 real label
진짜 데이터에 대해서는 real label에 대해서 다루고 가짜 데이터에 대해서는 fake label에 대해서 다뤄 오차를 최소화하는게 판별기의 목적
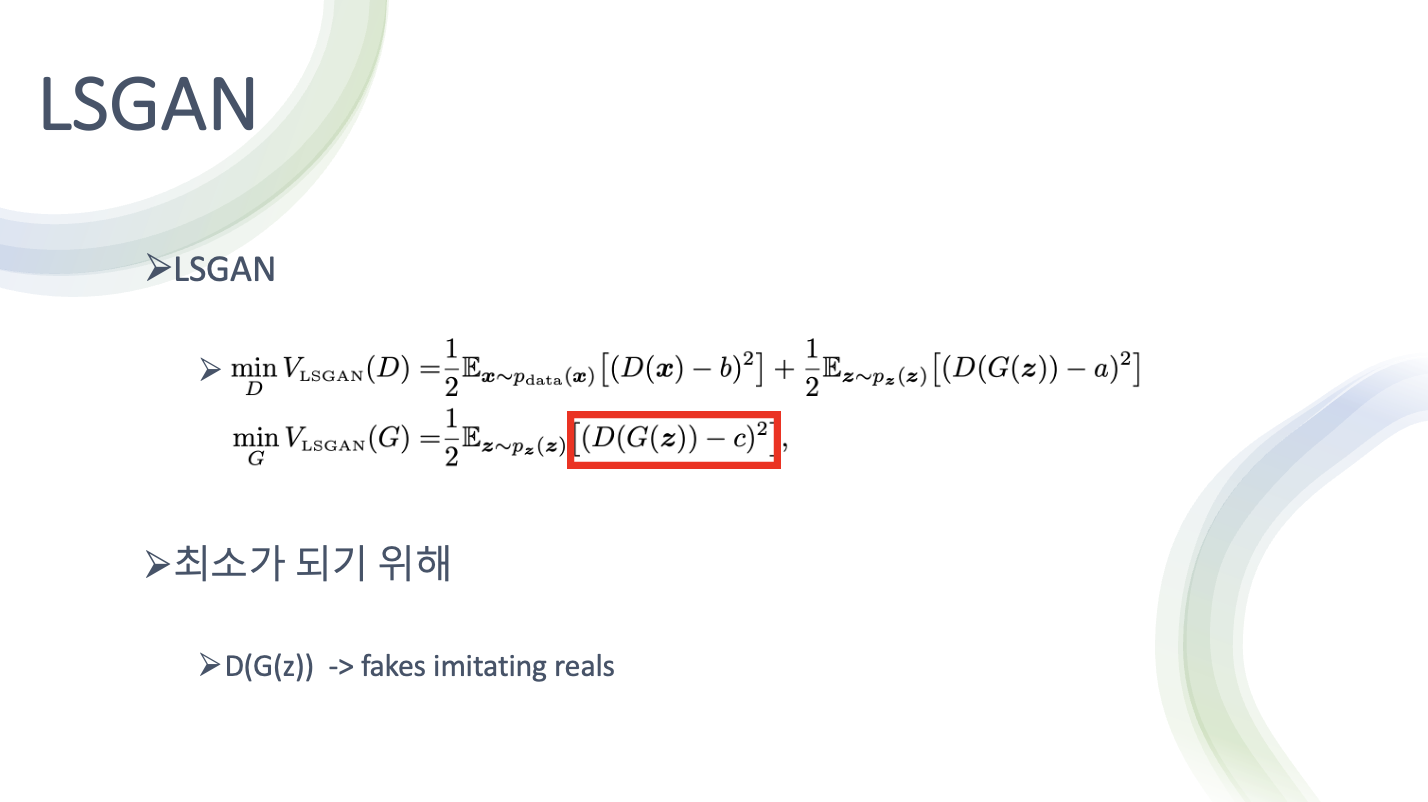
생성기는 real data에 대한 정보는 필요가 없고 자기가 만드는 fake data에 대한 정보만 있으면 되서 아래처럼 생김
- 여기서 a를 그냥 fake label이라고 말하고 있지만 c는 생성기 입장에서 진짜라고 믿게 하고싶은 fake 라는 요소가 있어서 기호를 다르게 표시
- D가 최소가 되기 위해서는 D가 판별한 값과 real data의 오차가 적어야 함
- 또한 G가 생성한 가짜 이미지를 D가 판별 했을 때 a와 가까워 져야 함
- G는 진짜를 흉내내는 fake들 에 가깝게 가서 손실을 최소화 해야 함
Relation to Pearson x^2 Divergence
원래의 GAN 논문에서는, 저자들은 Equation 1을 Jensen-Shannon divergnce를 최소화하는 것으로 만든다. 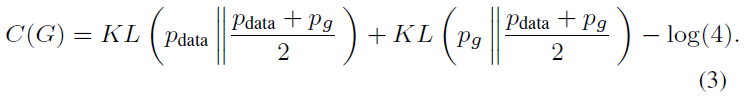
우리는 LSGAN과 f-divergence 사이의 관계를 탐험한다 Equation 2의 확장은 다음과 같이 따른다. 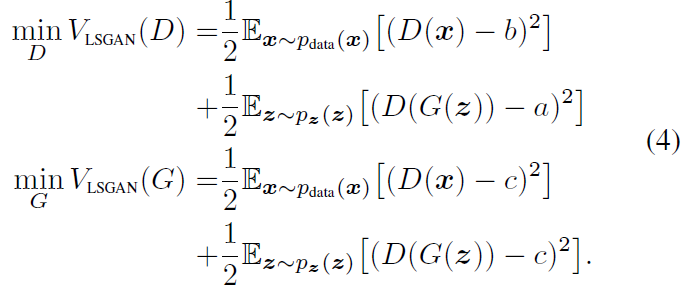
고정된 G의 최적의 discriminator D는 다음과 같이 유도된다. 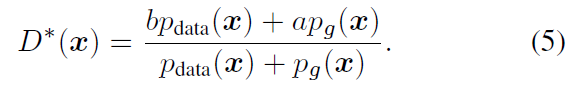
우리는 Equation 4의 V_LSGAN(G)를 재형성 할 수 있다. 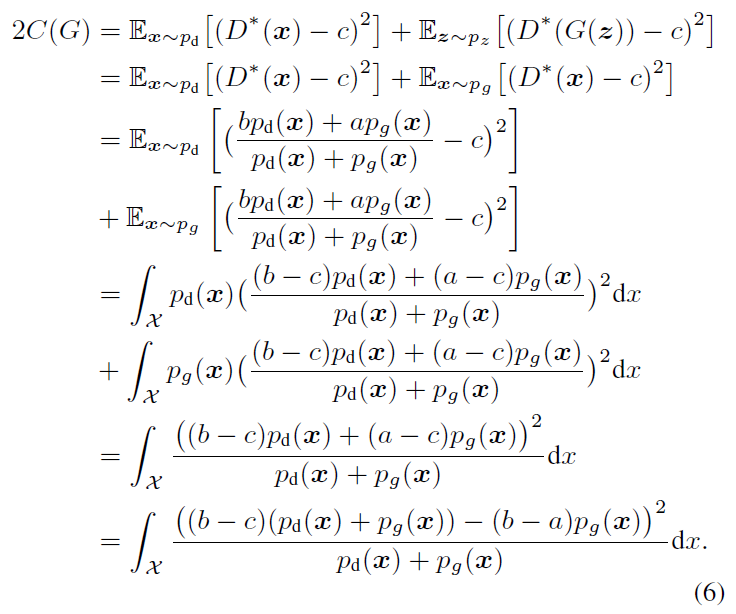
Parameters Selection
Equation 2에서 value a,b,c를 정의하기 위한 하나의 방법은 b-c=1, b-a=2의 조건을 만족시키는 것이다. 예를 들어, a=-1, b=1, c=0의 셋팅을 따르면 다음과 같은 목적함수를 얻을 수 있다. 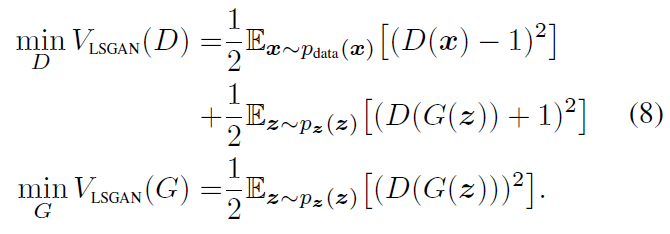
또 다른 방법은 c=b로 셋팅함으로써 생성하는 샘플들을 최대한 실제로 만드는 것이다. 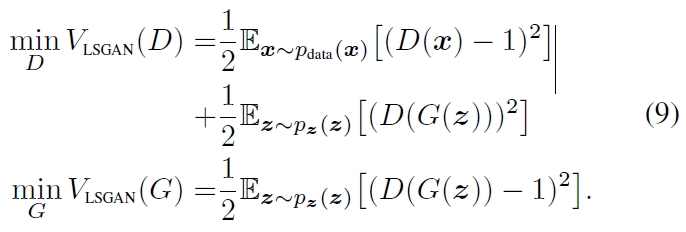
Model Archiectures
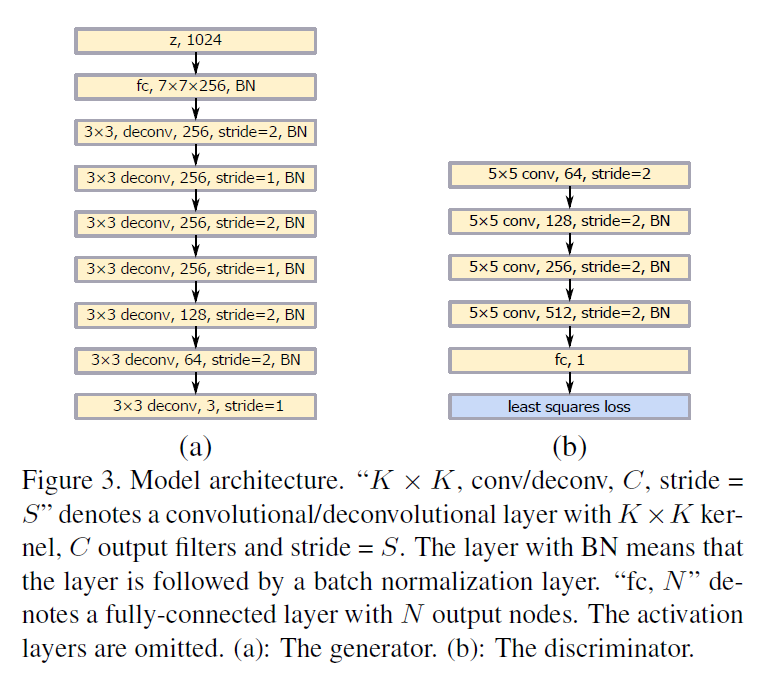
VGG model에 의해 동기부여된 우리가 설계한 첫번째 모델은 Figure 3에서 보여진다. [25]에서의 아키첵쳐와 비교하여, 두개의 stride=1 deconvolutional layers는 top two deconvolutional layer 후에 추가된다. discriminator의 아키텍쳐는 least square loss function의 사용을 제외하고 [25]에서의 것과 동일하다. DCGAN을 따르면, ReLU activation과 LeakyReLU activation은 각각 generator와 discriminator에 사용되었다.
우리가 설계한 두번째 모델은 예를 들어 중국어 같은 많은 클래스를 가진 과제를 위한 것이다. 중국어를 위해, 우리는 여러개의 클래스 에서 GAN을 학습하는 것은 읽을 수 있는 문자를 생성하는데 가능하지 않다는 것을 발견했다. 이유는 입력은 여러개의 클래스가 있지만, 출력은 하나의 클래스를 갖기 때문이다. [9]에서 말한데로, 입력과 출력간의 결정적인 관계가 있어야 한다. 이러한 문제를 푸는 방법 중 하나는 conditional GAN을 사용하는 것이고 레이블 정보를 조건화 하는 것은 입력과 출력 사이의 결정적인 관계를 생성하기 때문이다. 하지만, 수만개의 클래스의 one-hot encoding 레이블 벡터에서 직접적으로 조건화하는 것은 메모리 비용과 계산량 측면에서 불가능하다. 우리는 레이블 벡터의 차원을 줄이기 위해서 선형 맵핑 레이어를 사용한다. generator를 위해, 레이블 벡터는 노이즈 입력 레이어로 concatenated 된다. discriminator를 위해, 레이블 벡터는 모든 convolutional layer와 fully-connected layer에 concatenate 된다. concatenated된 레이어들은 실험적으로 결정된다.
DCGAN 해상도도 낮고 많이 부자연스러운 요소가 많음
LSGAN은 상대적으로 더 선명하고 DCGAN보다 더 나은 방 이미지를 생성함
왜냐하면 DCGAN은 이미 진짜로 판단된 fake이미지에 대해서는 업데이트 할 수 있는 정보를 얻을 수 없지만 LSGAN은 진짜로 분류된 fake 이미지에 대해서도 결정경계에 더 가깝게 만들어 주기 위해, 진짜 분포와 비슷하게 만들기 위해 손실을 설계했기 때문에 진짜에 가까운 데이터를 생성하게 됨
- LSGAN이 생성한 다양한 이미지들
또 다른 실험은 [19]에서 설계된 Gaussian mixture distribution 데이터셋에서 평가하는 것이다. 우리는 LSGAN과 보통의 GAN을 generator와 discriminator 둘다 3개의 fully connected layer를 가지고 있는 간단한 네트워크 아키텍쳐를 사용하여 2D mixture of 8 Gaussian 데이터셋에서 학습했다. Figure 7은 Gaussian kernel density estimation의 동적인 결과를 보여준다. 우리는 보통의 GAN이 step 15k에서 시작해서 mode collapse를 겪는 것을 볼 수 있다. 이것들은 데이터 분포의 하나의 유효한 mode 주위의 샘플을 생성한다. 하지만 LSGAN은 Gaussian mixture distribution을 성공적으로 학습한다.
Handwritten Chinese Characters
우리는 또한 conditional LSGAN 모델을 3740개의 클래스를 포함하는 중국어 손글씨 데이터셋에서 학습했다. LSGAN은 성공적으로 읽을 수 있는 중국어를 생성하도록 학습했고, 몇개의 랜덤하게 선택된 문자들이 Figure 8에서 보여진다. 우리는 Figure 8로부터 두개의 주요한 관찰을 얻었다. 첫번째로, LSGAN에 의해 생성된 문자들은 읽을 수 있다는 것이다. 두번째로, 우리는 data augmentation과 같이 더 나아간 어플리케이션에 사용될 수 있는 레이블 벡터를 통해 생성된 이미지의 정확한 레이블을 얻을 수 있다.
LSGAN 요약
LSGAN의 가장 중요한 부분은 그 목적 함수의 변형에 있으며, 이는 생성된 데이터의 품질을 향상시키고, 모드 붕괴(mode collapse) 문제를 완화하는 데 도움을 준다.
LSGAN의 핵심 요약:
목적 함수의 변형: LSGAN은 전통적인 GAN에서 사용되는 크로스 엔트로피 손실 대신, least squares loss function (최소 제곱 손실 함수)를 사용. 이 변경은 학습 과정의 안정성을 높이고, 생성된 이미지의 품질을 개선하는 데 목적이 있다.
손실 공식의 차이: LSGAN에서는 실제 데이터에 대한 판별자의 출력을 1에 가깝게, 생성된 데이터에 대한 출력을 0에 가깝게 만들려고 한다. 이는 생성자와 판별자 사이의 거리를 최소화하는 것을 목표로 한다.
Loss 공식:
LSGAN의 손실 함수:
MSE 기반 손실함수: $\frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2$
판별자 손실 (Discriminator Loss): $L_D = \frac{1}{2} \mathbb{E}{x \sim p{data}(x)}[(D(x) - b)^2] + \frac{1}{2} \mathbb{E}_{z \sim p_z(z)}[(D(G(z)) - a)^2]$
생성자 손실 (Generator Loss): $L_G = \frac{1}{2} \mathbb{E}_{z \sim p_z(z)}[(D(G(z)) - c)^2]$
여기서:
- $D(x)$는 판별자의 출력
- $G(z)$는 생성자가 입력 $z$로부터 생성한 데이터
- $a$, $b$, $c$는 레이블의 값을 지정하는 상수이며, 일반적으로 $a=0$, $b=c=1$로 설정. 이는 판별자가 실제 이미지를 얼마나 정확하게 진짜로 판별하고, 생성된 이미지를 가짜로 판별하는지를 측정.
이 손실 함수를 통해 LSGAN은 판별자와 생성자 간의 경쟁을 통해 학습이 이루어지며, 이 과정에서 생성된 이미지의 질을 향상시킨다. LSGAN의 목적 함수는 생성된 데이터와 실제 데이터 사이의 거리를 최소화하려고 시도하며, 이는 결과적으로 더 안정적인 학습 과정과 높은 품질의 생성 이미지로 이어진다.
LSGAN의 목적 함수와 GAN과의 차이
GAN의 목적 함수는 크로스 엔트로피 손실을 기반으로 하며, 이는 두 부분으로 구성됩니다: 생성자(generator)의 손실 함수와 판별자(discriminator)의 손실 함수
판별자 손실 (Discriminator Loss): $L_D = -\mathbb{E}{x \sim p{data}(x)}[\log(D(x))] - \mathbb{E}_{z \sim p_z(z)}[\log(1 - D(G(z)))]$
생성자 손실 (Generator Loss): $L_G = -\mathbb{E}_{z \sim p_z(z)}[\log(D(G(z)))]$
여기서 $D(x)$는 판별자가 실제 데이터 $x$를 진짜로 인식할 확률을, $G(z)$는 생성자가 노이즈 $z$로부터 생성한 데이터를 나타낸다.
LSGAN은 목적 함수로 최소 제곱 손실(least squares loss)을 사용하여, 결과적으로 더 부드러운 그래디언트를 제공하고, 학습 과정에서의 안정성을 개선.
- 판별자와 생성자 손실:
- LSGAN은 $a$, $b$, $c$ 값을 사용하여 손실을 계산하는데, 여기서 $a$, $b$, $c$ 는 레이블 값으로, 통상적으로 $a=0$, $b=c=1$로 설정
- GAN은 로그 확률을 사용하여 진짜와 가짜를 구분하는 판별자의 능력과 생성자가 판별자를 속이려는 능력을 측정
$\frac{1}{2}$가 앞에 붙는 이유
LSGAN의 손실 함수에서 $\frac{1}{2}$는 손실 값의 스케일을 조정하기 위해 사용. 이 계수는 최소 제곱 손실 함수의 그래디언트를 계산할 때 발생하는 2를 상쇄하기 위한 것. 최소 제곱 손실을 미분할 때, $2(x - y)$ 형태의 항이 나타나는데, 여기서 $\frac{1}{2}$를 곱함으로써 최종 그래디언트 값을 조정하고, 학습 과정에서의 그래디언트 폭발을 방지. 이는 학습 과정을 더 안정적으로 만들고, 학습 속도를 개선하는 데 도움을 준다.
하지만
$\frac{1}{2}$을 곱하는 것은 수학적으로 손실 함수의 미분 과정에서 발생하는 2를 상쇄하기 위한 것이지만, 실제 신경망 학습에서는 이 계수를 생략해도 상관 없다.
학습률 조정 가능: 신경망을 학습할 때, 학습률(learning rate)은 모델 가중치의 업데이트 크기를 결정한다. 손실 함수 앞에 $\frac{1}{2}$을 곱하든 안 하든, 학습률을 조절함으로써 모델 학습의 효과를 유사하게 조정할 수 있다.
실제 영향 최소화: 손실 함수의 절대값이 아닌, 그래디언트(기울기)의 방향과 크기가 모델 학습에 중요하다. $\frac{1}{2}$을 곱하는 것은 손실 값의 스케일을 조정할 뿐, 그래디언트의 방향에는 영향을 주지 않는다.
구현의 간결성: 많은 딥러닝 구현에서는 코드의 간결성과 이해의 용이성을 위해 불필요한 계수를 생략한다. $\frac{1}{2}$ 같은 상수를 곱하는 것이 학습 과정의 본질적인 부분에 큰 변화를 주지 않는 한, 생략하여도 모델 성능에 큰 영향을 미치지 않는다.
요약
- GAN은 크로스 엔트로피 손실을 사용하여 판별자와 생성자의 학습을 지휘.
- LSGAN은 최소 제곱 손실을 사용하여 더 안정적인 학습과 높은 품질의 이미지 생성을 목표.
- LSGAN의 손실 함수에 $\frac{1}{2}$를 곱하는 것은 미분 과정에서 나타나는 계수를 조정하고 학습 과정을 안정화하기 위한 것.
- 구현 시 $\frac{1}{2}$을 곱하는 것은 선택적.
구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import argparse
import os
import numpy as np
import math
import cv2
import matplotlib.pyplot as plt
import torchvision.transforms as transforms
from torchvision.utils import save_image
from torch.utils.data import DataLoader
from torchvision import datasets
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F
import torch
os.makedirs("images", exist_ok=True)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
"""
Adam 옵티마이저에서 b1과 b2는 그래디언트의 일차 및 이차 모멘텀 감쇠에 대한 매개변수.
- b1 (일차 모멘텀 감쇠): 일차 모멘텀 감쇠는 이전 그래디언트의 일차 모멘텀을 보존하는 데 사용.
일반적으로 0.9와 같은 값으로 설정
높은 값은 이전 그래디언트의 영향을 크게 받게 되어 더 많은 기억을 유지.
- b2 (이차 모멘텀 감쇠): 이차 모멘텀 감쇠는 이전 그래디언트의 이차 모멘텀을 보존하는 데 사용.
일반적으로 0.999와 같은 값으로 설정.
일차 모멘텀 감쇠와 마찬가지로, 높은 값은 이전 그래디언트의 영향을 크게 받게 되어 더 많은 기억을 유지.
"""
class Option():
n_epochs = 200 # 훈련할 에포크 수
batch_size = 64 # 배치의 크기
lr = 0.0002 # Adam 옵티마이저의 학습률
b1 = 0.5 # Adam 옵티마이저의 그래디언트의 일차 모멘텀 감쇠
b2 = 0.999 # Adam 옵티마이저의 그래디언트의 이차 모멘텀 감쇠
n_cpu = 8 # 배치 생성 중에 사용할 CPU 스레드 수
latent_dim = 100 # 잠재 공간의 차원
img_size = 32 # 각 이미지 차원의 크기
channels = 1 # 이미지 채널 수
sample_interval = 500 # 이미지 샘플링 간격
opt = Option()
# CUDA를 사용할 수 있는 경우 True, 그렇지 않은 경우 False로 설정
cuda = True if torch.cuda.is_available() else False
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
# 생성자 클래스 정의
class Generator(nn.Module):
def __init__(self):
super(Generator, self).__init__()
# 이미지 크기의 1/4로 초기값 설정
"""
`opt.img_size`는 원본 이미지의 크기.
`// 4` 연산은 이미지 크기를 4로 나누어 초기 크기를 설정.
이는 생성 과정에서 이미지를 점진적으로 업샘플링할 때의 시작 크기를 결정.
img_size = 32
"""
self.init_size = opt.img_size // 4 # 32 // 4 = 8
# 입력으로 사용되는 잠재공간 벡터를 초기값 크기의 128 채널 이미지로 변환하는 선형 레이어
"""
`opt.latent_dim`은 잠재 벡터의 차원을 나타낸다.
`nn.Linear`은 잠재 벡터를 입력으로 받아 고정된 크기의 벡터로 변환.
이 크기는 `128 * self.init_size ** 2`로, 변환된 벡터는 나중에 초기 이미지 차원으로 재배치.
latent_dim = 100
"""
# `128 * 8 * 8` 즉, 8192 차원 벡터(in_channels = 100, out_channels = 8192)
self.l1 = nn.Sequential(nn.Linear(opt.latent_dim, 128 * self.init_size ** 2))
# 컨볼루션 블록 정의. Upsampling을 통해 이미지를 점진적으로 확대하고,
# 각 단계에서 특징맵을 생성하고 정규화하며, LeakyReLU 활성화 함수를 사용.
self.conv_blocks = nn.Sequential(
nn.Upsample(scale_factor=2),
nn.Conv2d(128, 128, 3, stride=1, padding=1),
nn.BatchNorm2d(128, 0.8),
nn.LeakyReLU(0.2, inplace=True),
nn.Upsample(scale_factor=2),
nn.Conv2d(128, 64, 3, stride=1, padding=1),
nn.BatchNorm2d(64, 0.8),
nn.LeakyReLU(0.2, inplace=True),
nn.Conv2d(64, opt.channels, 3, stride=1, padding=1),
# 생성된 이미지 픽셀 값을 [-1, 1] 범위로 조정
nn.Tanh(),
)
# 순방향 패스 정의. 입력 잠재 벡터를 이미지로 변환.
def forward(self, z):
out = self.l1(z) # (batch_size, 8192)
"""
`view` 메서드는 `l1`에서의 출력 벡터를 4차원 텐서로 재배치.
여기서 첫 번째 차원은 배치 크기(batch size), 두 번째는 채널 수(여기서는 128), 세 번째와 네 번째는 이미지의 높이와 너비.
"""
out = out.view(out.shape[0], 128, self.init_size, self.init_size) # (64, 128, 8, 8)
img = self.conv_blocks(out) # (64, 1, 32, 32)
return img
# 판별자 클래스 정의
class Discriminator(nn.Module):
def __init__(self):
super(Discriminator, self).__init__()
# 판별자 블록 정의. 컨볼루션을 사용해 이미지를 점진적으로 축소하고, 특징맵을 생성하고 정규화하며, LeakyReLU 활성화 함수를 사용.
def discriminator_block(in_filters, out_filters, bn=True):
block = [nn.Conv2d(in_filters, out_filters, 3, 2, 1),
nn.LeakyReLU(0.2, inplace=True), nn.Dropout2d(0.25)]
if bn:
block.append(nn.BatchNorm2d(out_filters, 0.8))
return block
# 판별자 모델 정의. 컨볼루션 블록을 연결하여 이미지를 다운샘플링하고, 특징을 추출.
"""
코드에서 `*` 기호는 Python의 argument unpacking 연산자로 이 연산자는 리스트,
튜플 또는 다른 iterable 객체의 요소를 개별적으로 반환한다.
여기서는 `discriminator_block` 함수가 리스트를 반환하고,
그 리스트의 요소들을 `nn.Sequential`에 개별적으로 전달하기 위해 사용되었다.
`*`를 사용하지 않으면, `discriminator_block` 함수의 결과가 리스트로 감싸져서 전달되어, 예상한 대로 작동하지 않게 된다.
"""
self.model = nn.Sequential(
# input = (64, 1, 32, 32)
*discriminator_block(opt.channels, 16, bn=False), # (64, 16, 16, 16)
*discriminator_block(16, 32), # (64, 32, 8, 8)
*discriminator_block(32, 64), # (64, 64, 4, 4)
*discriminator_block(64, 128), # (64, 128, 2, 2)
)
# 다운샘플링된 이미지의 높이와 너비
"""
입력 이미지가 판별자를 통과하면서 4번의 다운샘플링을 거친다.
최종 다운샘플링된 이미지의 크기를 계산하기 위해 원본 이미지 크기를 2의 4승으로 나눈다.
img_size = 32
"""
ds_size = opt.img_size // 2 ** 4 # 32 // 16 = 2
# 입력 이미지의 진위를 판별하는 선형 레이어
"""
`adv_layer`는 판별자의 최종 층으로,
다운샘플링된 이미지의 특성을 기반으로 이미지가 실제인지 (1) 아니면 가짜인지 (0)를 결정하는 하나의 출력 값을 생성.
"""
# in_channels = 128 * 4 (512)
# out_channels = 1
self.adv_layer = nn.Linear(128 * ds_size ** 2, 1)
# 순방향 패스 정의. 입력 이미지가 실제 이미지인지 생성된 이미지인지 판별.
def forward(self, img):
out = self.model(img) # (64, 128, 2, 2)
out = out.view(out.shape[0], -1) # (64, (128 * 2 * 2)512)
validity = self.adv_layer(out) # (64, 1)
return validity
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
# 평균 제곱 오차(Mean Square Error, MSE)를 사용하여 손실을 계산하는 오브젝트를 생성
adversarial_loss = torch.nn.MSELoss()
# Generator와 Discriminator 클래스의 인스턴스 생성
generator = Generator()
discriminator = Discriminator()
# CUDA를 사용할 수 있는 경우, 모델과 손실 함수를 GPU 메모리로 이동
if cuda:
generator.cuda()
discriminator.cuda()
adversarial_loss.cuda()
def weights_init_normal(m):
classname = m.__class__.__name__
# 클래스 이름에 "Conv"가 포함되어 있을 경우,
if classname.find("Conv") != -1:
# 가중치 값을 평균 0.0, 표준 편차 0.02로 정규 분포에서 초기화
torch.nn.init.normal_(m.weight.data, 0.0, 0.02)
# 클래스 이름에 "BatchNorm"이 포함되어 있을 경우
elif classname.find("BatchNorm") != -1:
# 가중치 값을 평균 1.0, 표준 편차 0.02로 정규 분포에서 초기화
torch.nn.init.normal_(m.weight.data, 1.0, 0.02)
# 편향 값을 0으로 초기화
torch.nn.init.constant_(m.bias.data, 0.0)
# 모델의 가중치를 초기화. weights_init_normal은 정규 분포를 사용하여 가중치를 초기화하는 함수.
generator.apply(weights_init_normal)
discriminator.apply(weights_init_normal)
# 데이타셋을 로드하고, 전처리를 적용한 후, 배치 단위로 데이터를 제공하는 DataLoader를 생성.
os.makedirs("dataset/mnist", exist_ok=True)
dataloader = torch.utils.data.DataLoader(
datasets.MNIST(
"dataset/mnist",
train=True,
download=False,
transform=transforms.Compose(
[
transforms.Resize(opt.img_size),
transforms.ToTensor(),
transforms.Normalize([0.5], [0.5])
]
),
),
batch_size=opt.batch_size,
shuffle=True,
)
# Adam 최적화기를 사용하여 각 모델의 파라미터를 업데이트. 학습률(lr)과 베타 파라미터(b1, b2)는 옵션에서 가져온다.
optimizer_G = torch.optim.Adam(generator.parameters(), lr=opt.lr, betas=(opt.b1, opt.b2))
optimizer_D = torch.optim.Adam(discriminator.parameters(), lr=opt.lr, betas=(opt.b1, opt.b2))
# cuda를 사용할 수 있는 경우 Tensor를 GPU에, 그렇지 않으면 CPU에 할당.
# 이 Tensor는 후에 잠재 공간 벡터를 생성하거나 real/fake 레이블을 생성하는 데 사용.
Tensor = torch.cuda.FloatTensor if cuda else torch.FloatTensor
LSGAN 손실 함수:
MSE 기반 손실함수: $\frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2$
판별자 손실 (Discriminator Loss): $L_D = \frac{1}{2} \mathbb{E}{x \sim p{data}(x)}[(D(x) - b)^2] + \frac{1}{2} \mathbb{E}_{z \sim p_z(z)}[(D(G(z)) - a)^2]$
생성자 손실 (Generator Loss): $L_G = \frac{1}{2} \mathbb{E}_{z \sim p_z(z)}[(D(G(z)) - c)^2]$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
# 전체 에폭에 대해 반복. 한 에폭은 전체 데이터셋을 한 번 학습하는 것을 의미.
for epoch in range(opt.n_epochs):
# DataLoader는 배치 단위로 데이터를 제공. 각 배치에 대해 반복.
for i, (imgs, _) in enumerate(dataloader):
# 실제 이미지에 대한 레이블을 1로, 생성된 이미지에 대한 레이블을 0으로 설정.
valid = Variable(Tensor(imgs.shape[0], 1).fill_(1.0), requires_grad=False)
fake = Variable(Tensor(imgs.shape[0], 1).fill_(0.0), requires_grad=False)
# 실제 이미지를 Tensor로 변환.
real_imgs = Variable(imgs.type(Tensor))
# -----------------
# Train Generator
# -----------------
# 생성자의 그래디언트를 초기화.
optimizer_G.zero_grad()
# 잠재 공간에서 가우시안 랜덤 벡터를 샘플링. 이 벡터는 생성자의 입력으로 사용.
z = Variable(Tensor(np.random.normal(0, 1, (imgs.shape[0], opt.latent_dim))))
# 샘플링한 벡터를 사용해 생성자가 이미지를 생성하게 한다.
gen_imgs = generator(z)
# 생성자의 손실을 계산. 이 손실은 생성자가 판별자를 얼마나 잘 속였는지를 측정.
g_loss = adversarial_loss(discriminator(gen_imgs), valid)
# 생성자의 그래디언트를 계산하고, 그래디언트를 사용해 생성자의 파라미터를 업데이트.
g_loss.backward()
optimizer_G.step()
# ---------------------
# Train Discriminator
# ---------------------
# 판별자의 그래디언트를 초기화.
optimizer_D.zero_grad()
# 판별자의 손실을 계산. 이 손실은 판별자가 실제 이미지와 생성된 이미지를 얼마나 잘 구별하는지를 측정.
real_loss = adversarial_loss(discriminator(real_imgs), valid)
fake_loss = adversarial_loss(discriminator(gen_imgs.detach()), fake)
d_loss = 0.5 * (real_loss + fake_loss)
# 판별자의 그래디언트를 계산하고, 그래디언트를 사용해 판별자의 파라미터를 업데이트.
d_loss.backward()
optimizer_D.step()
# 현재까지 처리한 배치의 수를 계산.
batches_done = epoch * len(dataloader) + i
# 500 step 간격으로 로그를 출력하고, 생성된 이미지를 저장.
if batches_done % opt.sample_interval == 0:
print(
"[Epoch %d/%d] [Batch %d/%d] [D loss: %f] [G loss: %f]"
% (epoch, opt.n_epochs, i, len(dataloader), d_loss.item(), g_loss.item())
)
save_image(gen_imgs.data[:25], "images/%d.png" % batches_done, nrow=5, normalize=True)
# 생성된 이미지를 출력.
plt.figure(figsize = (5,5))
img1 = cv2.imread("images/%d.png" %batches_done)
plt.imshow(img1, interpolation='nearest')
plt.axis('off')
plt.show()