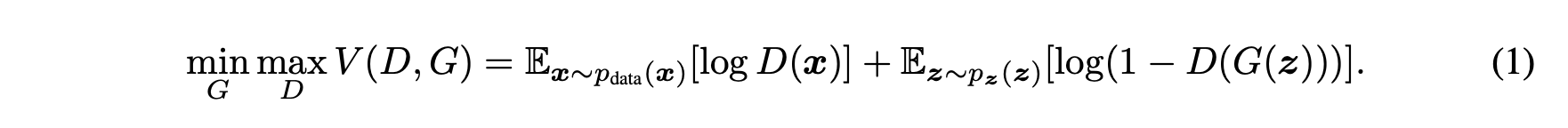GAN 논문 리뷰
| 태그 | #GenerativeModel |
|---|---|
| 한줄요약 | GAN |
| Journal/Conference | #NIPS |
| Link | GAN |
| Year(출판년도) | 2014 |
| 저자 | I. Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron C. Courville, Yoshua Bengio |
| 원문 링크 | GAN |
핵심 요약
- 적대적으로 동작하는 두개의 네트워크를 사용해 새로운 데이터를 생성할 수 있는 GAN(Generative Adversarial Nets) 구조를 제안한다.
- 생성자(Generator) 와 판별자(Discriminator) 모두 마르코프 체인 등의 구조없이 back-propagation 으로 학습이 가능한 인공신경망 구조를 사용한다.
- 이후 등장하는 수많은 GAN 기반 모델의 기원이 되는 논문이다.
Introduction & Related Works
분류 문제에 제한되어 사용되던 딥러닝 모델의 용도를 새로운 데이터를 생성하는 문제에도 적용할 수 있는 적대적 생성 신경망(Generative Adversarial Nets)을 최초로 제시한 논문이다.
GAN은 아래와 같은 목표를 가진, 적대적인 두 모델을 학습한다.
- 판별자(Discriminator) 모델
- 데이터가 원본 데이터셋에서 온것인지, 생성자가 만든 것인지를 판별
- 예시) 경찰이 지폐가 위조되었는지를 판별
- 생성자(Generator) 모델
- 감별자가 구분할 수 없는 가짜 데이터를 생성
- 예시) 위폐범이 경찰이 구분할 수 없는 위조 지폐를 제작함
논문은 해당 방법이 특별한 모델이나 학습 방법을 필요로 하지 않는 방법이라고 하며, MLP(multi-layer perception) 구조를 사용해 학습한 결과를 소개한다.
Adversarial nets
적대적 신경망의 가장 직관적인 예시로 MLP 모델을 사용한 경우를 가정하여 설명합니다. 이 때 사용하는 표기법은 다음과 같다.
- $x\sim p_{data}$ : 실제 데이터로부터 뽑은 샘플
- $p_g$ : 생성자가 생성하는 데이터의 분포
- $p_z(z)$ : 데이터를 생성하기 위해 사용하는 입력 노이즈 분포
- $G(z;\theta_g)$ : 생성자 모델
- $\theta_g$ : 생성자 모델 파라미터
- $D(x;\theta_d)$ : 감별자 모델
- $\theta_D$ : 감별자 모델 파라미터
D 는 실제 데이터와 생성된 데이터에 정확히 구분할 수 있는 확률을 최대화 하려고 한다. G 는 D가 실제 데이터로 착각할 만한 데이터를 생성하는 것을 목적으로 $\log(1-D(G(z)))$ 를 최소화 하려고 한다.
따라서 아래와 같이 가치함수 $V(G,D)$ 가 주어졌을 때, G 는 최소화를 D는 최대화를 목적으로 경쟁한다.
실제 계산에서 V 를 최대로 하는 D 를 구할 때 많은 계산이 필요하고, 데이터셋이 제한된 상황에서 과적합이 발생할 수도 있습니다. 따라서 실제 훈련에서는 D 를 k 번만 학습하고 G 를 학습한다.
또한, 학습 초기에는 G가 생성하는 데이터의 품질이 낮으므로 D가 판별을 하기 쉬워, $\log(1−D(G(z)))$ 항이 소실될수 있다. 따라서, $\log D(G(z))$ 를 최대화 하는 문제로 변환하여 초기에 학습이 잘 이뤄질 수 있도록 한다.
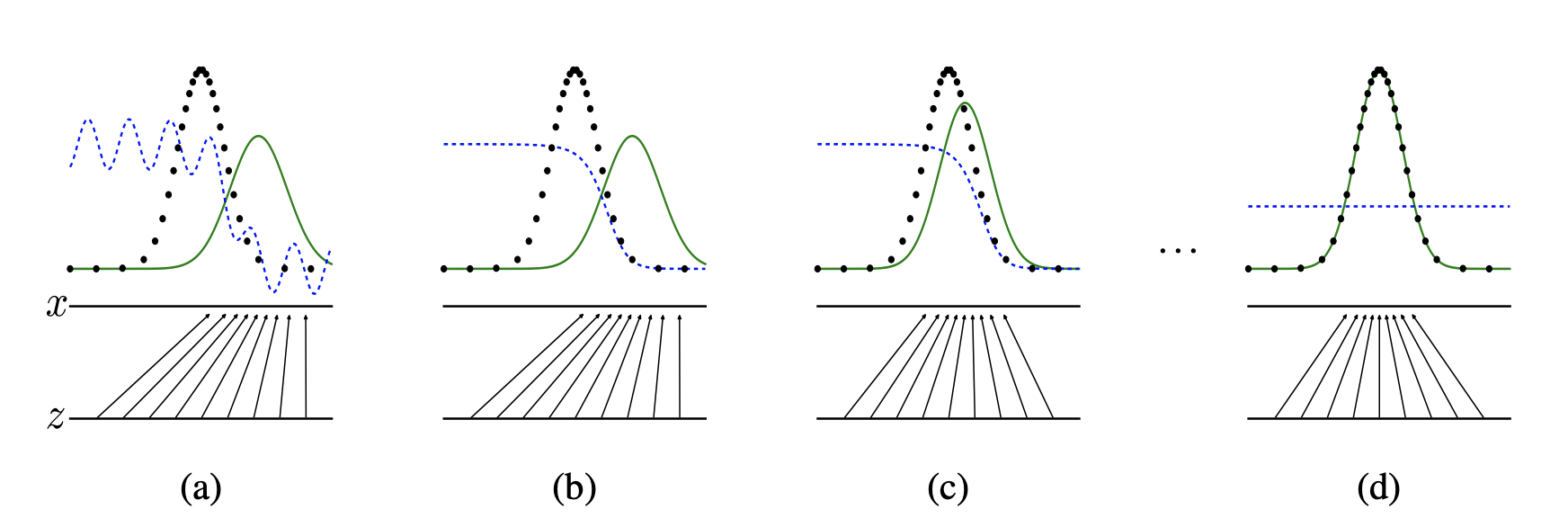
학습 과정의 모식도입니다. 파란 점선은 감별자 D의 분포, 검은 점은 원본 데이터 분포, 초록 실선은 생성자 G의 분포를 나타낸다.
(a) 와 같이 학습이 완료되기 전의 상태에서 시작한다.
(b) 와 같이 D 를 업데이트 할 때, 최적의 D 는 $D_{G}^{*}(x)= \frac{p_{data}(x)}{p_{data}(x)+p_{g}(x)}$ 로 수렴한다.
(c) G를 업데이트하면, D 를 교란할 수 있도록 G 가 생성하는 분포가 실제 데이터 분포에 가까워진다.
(d) 학습 과정을 반복하면 생성자는 데이터 분포와 일치하는 데이터를 생성($p_g = p_{data}$) 하며, 감별자는 어떠한 샘플도 구분할 수 없게 된다. ($D(x)=\frac{1}{2}$)
Theoretical Results
적대적 신경망 문제에서 생성자가 원본 데이터와 유사한 분포의 데이터를 생성할 수 있다는 증명을 제시한다. 또한, 실제 적대적 신경망을 학습하기 위해 설계한 아래 알고리즘 또한 같은 결과에 수렴한다는 증명을 제시한다.
Global Optimality of $p_g = p_{data}$
먼저 임의의 G 가 주어졌을 때 최적의 D 를 계산하는 과정을 보입니다.
최적의 D 를 이용하여 Equation 1 을 G에 관한 수식으로 표현할 수 있다.
이 때 새롭게 정리한 가치함수가, G가 생성하는 데이터의 분포가 실제 분포를 따르는 경우에만 최소화된다는 것을 다음과 같이 증명한다.
Convergence of Algorithm 1
G 와 D 가 p_g 충분한 표현력을 갖고 있을 때, 제시한 알고리즘이 p_g=p_{data} 로 수렴함을 아래와 같이 증명한다.
실제로 MLP 를 사용한 G 로는 모든 형태의 p_g 를 표현할 수 없으므로 이론적인 최고 성능을 보장하기 어렵다. 논문은 그럼에도 불구하고 GAN이 실제 훈련결과에서 좋은 성능을 보임을 제시한다.
Experiments
실험에 사용한 조건은 다음과 같다.
- Dataset : MNIST, Toronto Face Database(TFD), CIFAR-10 사용
- Generator : ReLU/sigmoid 활성함수를 혼합하여 사용
- Discriminator : maxout 활성함수를 사용
- D를 학습시킬 때만 Dropout을 사용
- G에서 데이터를 생성하는 경우에만 noise를 input 으로 사용
GAN 은 데이터 분포 자체를 구하기 위한 tractable likelihood 를 가정하지 않는다. 이러한 모델을 평가하기 위해 기존에 제안된 방법은 다음과 같다.
- Generator 에서 생성한 데이터를 Gaussian Parzen window 에 fitting
- fitting 한 분포가 주어졌을 때 log-likelihood 를 계산
- Validation set 으로 교차 검증을 수행해 표준 편차를 계산
논문은 해당 방법의 분산이 크고 높은 차원의 데이터에서 잘 작동하지 않지만, GAN 이 기존 모델에 비해 상대적으로 좋은 결과를 보이고 있음을 제시한다.
또한 위 그림과 같이, Generator 의 Input noise 를 점진적으로 변형시킬 때, 점점 interploation 되어가는 생성 데이터를 확인할 수 있다.
Advantages and disadvantages
GAN 의 단점
- Generator 가 생성하는 데이터의 분포가 명시적으로 존재하지 않는다.
- Generator 와 Discriminator 의 균형이 깨지는 경우 학습이 원활이 이루어지지 않는다.
또한, GAN 의 장점
- 마르코프 체인 같은 구조 없이 역전파 만으로도 학습이 가능하다.
- Generator 의 분포로 특별한 모델을 가정하지 않는다.
- 더욱 복잡한 데이터 분포를 모사할 수 있어 선명한 데이터를 생성할 수 있다.
Conclusions and future work
GAN 프레임워크를 확장하고 개선할 수 있는 다양한 방법을 제시한다.
- 주어진 조건에 따라 데이터를 생성하는 모델로 발전 가능
- x가 주어졌을 때 z를 예측하는 보조 네트워크를 학습한다면 생성자의 데이터 분포를 예측할 수 있음
- parameters를 공유하는 conditionals model를 학습함으로써 다른 conditionals models을 근사적으로 모델링할 수 있음
- Semi-supervised learning에도 활용 가능 : 데이터가 제한된 경우 Discriminator 를 활용하여 classifier의 성능을 향상시킬 수 있음
- 효율성 개선: G와 D를 균형있게 학습할 수 있는 방법이나 새로운 z 분포를 제시하여 학습 속도 개선 가능