1. GAN 이론
이미지 생성 원리
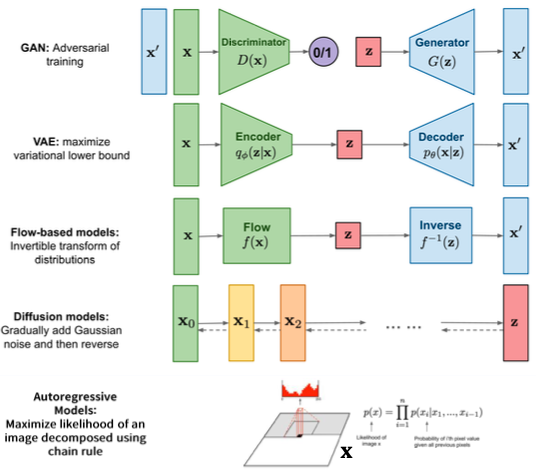
GAN (Generative Adversarial Network)은 딥러닝 모델 중 이미지 생성에 널리 쓰이는 모델
CNN은 이미지에서 개인지 고양이인지 구분하는 이미지 분류 문제에 쓰인다면 GAN은 모델이 데이터셋과 유사한 이미지를 만들도록 하는 것
- 이미지 생성 원리
경찰과 위조지폐범
위조지폐범은 위조지폐를 진짜 지폐와 거의 비슷하게 만들고 경찰은 이 지폐가 진짜 지폐인지 위조지폐인지 구분
위조지폐범과 경찰은 적대적인 관계에 있고, 위조지폐범은 계속 위조지폐를 생성하고 경찰은 진짜를 찾아내려고 하는 쫓고 쫓기는 과정이 반복
이때 위조지폐범(Generator)와 경찰(Discriminator)가 서로 위조지폐를 생성하고 구분하는 것을 반복하는 minmax game
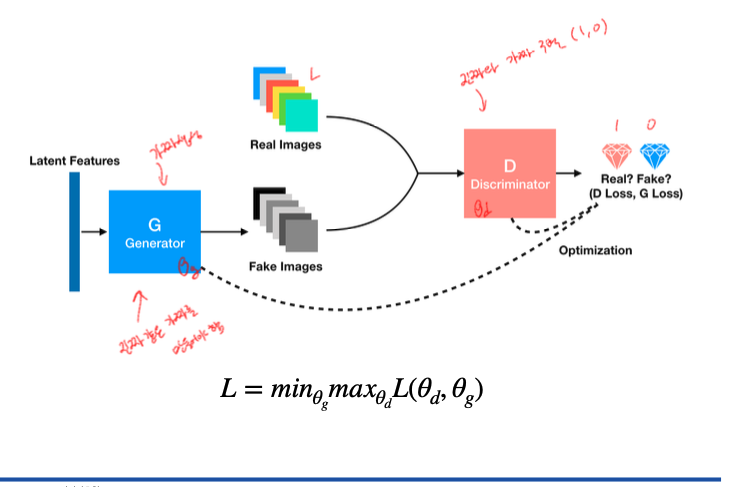
위와 마찬가지로 GAN또한 Generator(생성자)와 Discriminator(판별자) 두 개의 모델이 동시에 적대적인 과정으로 학습
생성자 G는 실제 데이터 분포를 학습하고, 판별자 D는 원래의 데이터인지 생성자로부터 생성된 것인지를 구분
생성자 G의 학습 과정은 이미지를 잘 생성해서 속일 확률을 높이고 판별자 D는 제대로 구분하는 확률을 높이는 두 플레이어의 minmax game의 과정
용어
- 기초 수학
- 확률분포
- 확률분포는 확률 변수가 특정한 값을 가질 확률을 나타내는 함수를 의미
- 예를 들어 주사위를 던졌을 때 나올 수 있는 수를 확률변수 X라고 하면
- 확률변수 X는 1, 2, 3, 4, 5, 6의 값을 가질 수 있다.
- P(X = 1)는 $\frac{1}{6}$
- P(X = 1) = P(X=2) = P(X=3) = P(X=4) = P(X=5) = P(X=6)
- 이산확률분포
- 확률변수 X의 개수를 정확히 셀 수 있을 때 이산확률분포라 말함
- 주사위 눈금 X의 확률 분포는 1 / 6이다
- 연속확률분포
- 확률변수 X의 개수를 정확히 셀 수 없을 때 연속확률분포라 말한다
- ex) 키, 달리기 성적
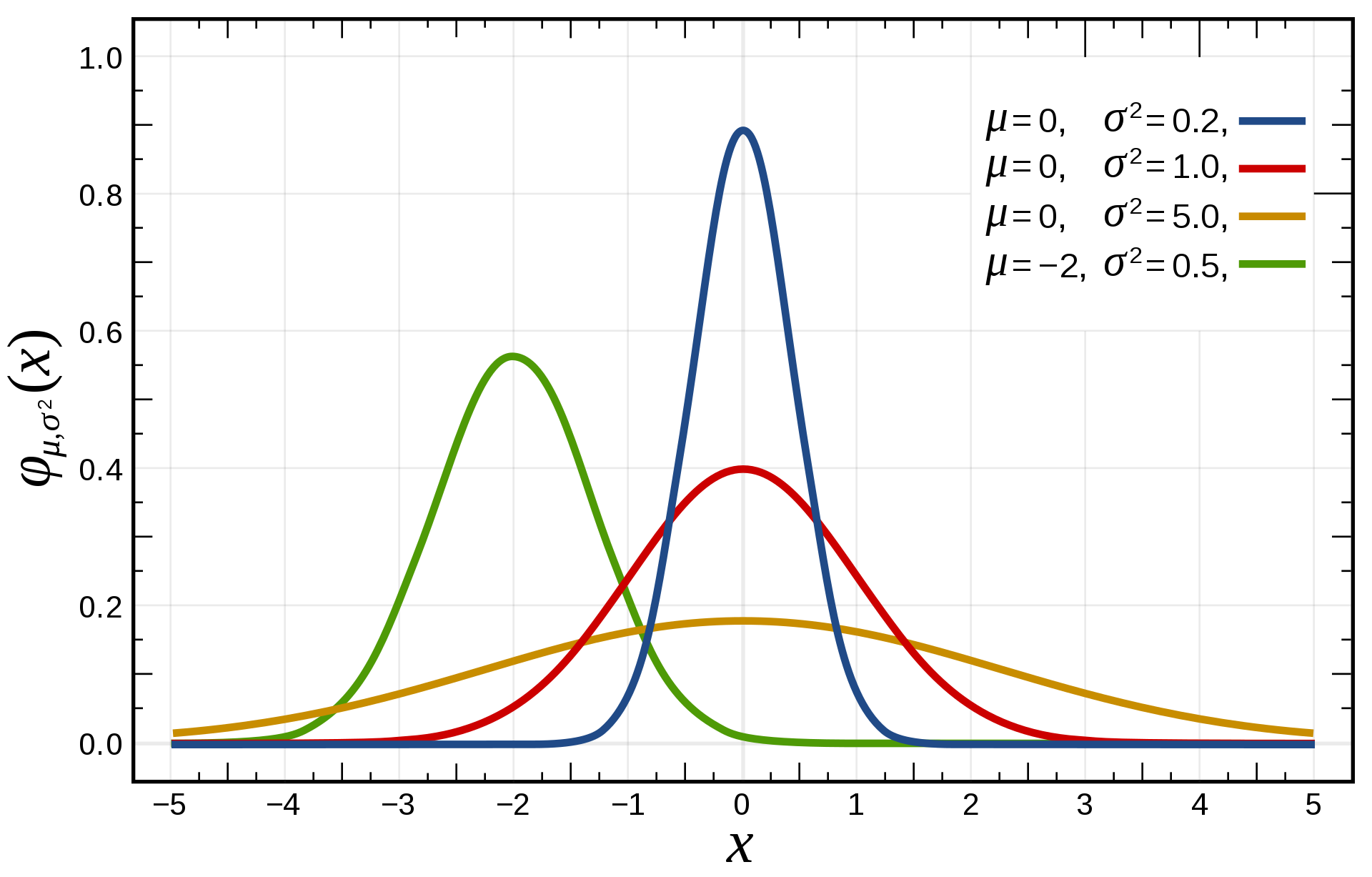
- 정규분포
- 수집된 자료의 분포를 근사하는데 주로 사용
- 가우시안 분포는 연속 확률 분포의 하나.
- 실제 세계 많은 데이터는 정규분포로 표현 가능
- 확률분포
- 이미지 데이터에 대한 확률분포
- 이미지 데이터는 다차원 특징 공간의 한 점으로 표현된다.
- 이미지의 분포를 근사하는 모델을 학습할 수 있다.
- 사람의 얼굴에는 통계적인 평균치가 존재할 수 있다.
- 모델은 이를 수치적으로 표현할 수 있게 된다.
- 이미지 데이터는 다차원 특징 공간의 한 점으로 표현된다.
- 생성 모델(Generative Models)
- 생성 모델은 실존하지 않지만 있을 법한 이미지를 생성할 수 있는 모델을 의미
- 생성 모델의 목표
- 이미지 데이터의 분포를 근사하는 모델 G를 만드는 것이 생성모델의 목표
- 모델 G가 잘 동작한다는 의미는 원래 이미지들의 분포를 잘 모델링할 수 있다는 것을 의미
- log 특성
- log(1) = 0
- log(0) = -infinity
- 게임이론 이란
- 폰 노이만과 오스카 모겐스턴에 의해 확립된 게임이론
게임이론은 사회전반에서 발생하는 개체와 개체간의 갈등, 경쟁, 대립, 협력등을 수학적 기법을 사용하여 표현하려는 수학의 한 분야
- 제로섬게임
- 승자의 이익과 패자의 손실을 합하면 항상 0
- ex) 가위바위보 : 누군가 이득이 있으면 그 반대는 항상 손실이 있다
- minimax game
- 누군가 이기면 누군가는 질 수밖에 없는 제로섬 게임에서는 지지 않는 것이 최선의 전략이지만 미니맥스 전략은 상대의 최대값을 최소화 하는것 혹은 졌을 때의 손실을 최소화 하는 것
- 맥스의 손실을 미니화 한다는 것
- 얘를들면 제로섬 게임의 대표적인 예인 고스톱에서 돈을 따기 위해서는 박부터 피하는 것이 기본인것 처럼 나보다 상대가 어떻게 하면 돈을 따지 못할까에 집중한 전략
주요 설명
Adversarial Nets
D and G play the following two-player minimax game with value functiuon $V(G,D):$
\[\min_{G} \; \max_{D} V(D, G) = E_{x \sim p_{data}} [\log D(x)] + E_{z \sim p_z(z)} [\log (1 - D(G(z)))]\]$D$는 $V$함수를 높이고자 vs $G$는 $V$함수를 낮추고자 경쟁 (Real : 1 ~ Fake : 0)
- 프로그램 상에서 기댓값(expected value)을 계산하는 방법
- = 단순히 모든 데이터를 하나씩 확인해 식에 대입한 뒤 평균값 계산
$E_{x \sim p_{data}} [\log D(x)]$ : 원본 데이터 분포 (data distrbution)에서의 sample $x$ 를 뽑아 $\log D(x)$ 의 기댓값 계산
$E_{z \sim p_z(z)} [\log (1 - D(G(z)))]$ : 노이즈 분포에서의 sample $z$ 를 뽑아 $\log (1-D(G(z)))$의 기댓값 계산
- 정리
- D의 입장
- 가짜 데이터에는 0을 출력, 진짜 데이터에는 1을 출력
- x는 진짜 데이터, G(z) 는 G가 z를 가지고 만든 가짜 데이터
따라서 D는 오른쪽 수식 중, D(x) = 1이 되어야 하고, D(G(z))는 0이 되도록 하는것이 최대 목표
- D가 가장 원하는 상황
$\min_{G} \; \max_{D} V(D, G) = E_{x \sim p_{data}} [\log D(x)] + E_{z \sim p_z(z)} [\log (1 - D(G(z)))]$ $logD(x)$ 에서 $D(x)$ = 1 $log(1-D(G(z)))$ 에서 $D(G(z))$ = 0 결국 0을 만드는게 가장 큰 값이며 D(G(z)) 가 0이 되는 상황이 D가 원하는 값 (Real : 1, Fake : 0)
따라서 D는 0에 가까운 숫자로 가기위해 노력하는 것을 $max$가 되려고 한다하고, 이를 $max\,D$로 표현한 것
G가 가장 원하는 상황
- $\min_{G} \; \max_{D} V(D, G) = E_{x \sim p_{data}} [\log D(x)] + E_{z \sim p_z(z)} [\log (1 - D(G(z)))]$
- G는 $E_{x \sim p_{data}} [\log D(x)]$ 는 관심없음
- 뒤에 있는 $D(G(z))$ 가 1 이 되도록 하는것이 목표 (Real : 1, Fake : 0)
- $log(1-1) = -infinity$
- 결국 G의 목표는 음의 무한대를 향하는 것이 목적
- 즉 G가 원하는 최적의 상황은 매우 작은 음의 무한대가 되는 방향
- D의 입장
Global Optimality of $p_g = P_{data}$
임의의 G가 주어졌을 때 최적의 D를 계산하는 과정 \(D_g^*(x) = \frac{P_{data}(x)}{P_{data}(x) + P_g(x)}\)
\[V(G, D) = E_{x \sim p_{data}} [\log D(x)] + E_{z \sim p_z(z)} [\log (1 - D(G(z)))]\]- 연속확률변수에 대한 기댓값 $E[X] = \int_{-\infty}^\infty xf(x)dx\; (x: 사건,\; f(x): 확률분포 함수)$ \(V(G,D) = \int_x \mathrm{p_{data}(x) \log(D(x))}\mathrm{d}x + \int_z p_z(z)log(1-D(G(z)))dz\)
z 도메인에서 Sampling된 noise vector를 G에 넣어서 데이터 x를 만들어낼 수 있고 이는 도메인 z에서 x로 맵핑되는 과정과 마친가지로 볼 수 있기 때문에 x로 치환해서 하나의 적분 식으로 표현 가능
\(= \int_x P_{data}(x) log(D(x)) + P_g(x)\log(1-D(x))dx\)
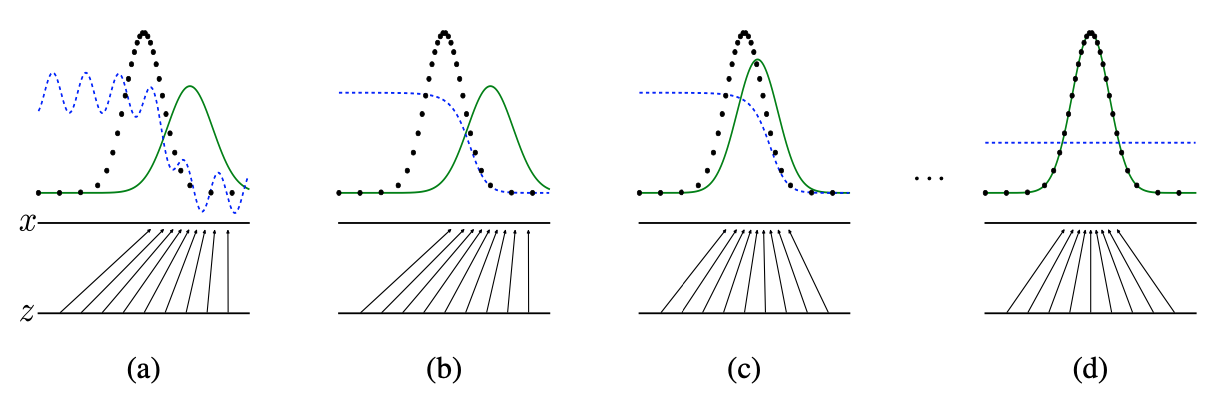
궁극적으로 알고자 하는 생성자의 Global optimum point는 어디인가
Proposition: $p_g = p_{data}$ (생성자의 분포는 원본 distribution을 따라가게 된다)
Proof: \(C(G) = \max_{d}V(G, D)\) \(= E_{x \sim p_{data}}[log(D^*(x)_G] + E_{z \sim p_z(z)}log(1-D^*_G(G(z)))]\)
\[=E_{x\sim p_{data}} [logD^*_G(x)] + E_{x \sim p_g} [log(1-D^*_G(x))]\] \[D^*_G(x) = {p_{data}(x) \over p_{data}(x) + p_g(x)}\]\(= E_{x\sim p_{data}(x)} \begin{bmatrix}log{P_{data}(x) \over p_{data}(x) + p_g(x)}\end{bmatrix} + E_{x \sim p_g(x)} \begin{bmatrix} log{p_g(x) \over p_{data}(x) + p_g(x)} \end{bmatrix}\) \(= E_{x \sim p_{data}(x)} \begin{bmatrix} log{2 \; * \; p_{data}(x) \over P_{data}(x) + p_g(x)}\end{bmatrix} + E_{x \sim p_g(x)} \begin{bmatrix} log {2 \; * \; p_g(x) \over P_{data}(x) + p_g(x)} \end{bmatrix} - log(4)\) 편의성을 위해 KL Divergence로 변환 (후에 Jensen-Shannon divergence로 변환)
- \[KL(p_{data} || p_g) = \int_{-\infty}^\infty p_{data}(x) log({p_{data}(x) \over p_g(x)}) dx\]
Kullback-Leibler divergence : 두개의 분포가 있을 떄 두 분포가 얼마나 차이가 나는지에 대한 내용을 수치적으로 표현하기 위해 일반적으로 사용할 수 있는 divergence 공식
- Jenson-Shannon divergence : 두개의 분포 p와 q가 있을 때 두 분포의 distance를 구하는데 사용 가능
KL divergence는 distance matric으로 활용 불가능 하지만 Jenson-Shannon divergence 는 distance matric 으로 활용 가능하므로 JSD로 변환
JSD 공식 \(JSD(p||q) = {1 \over 2}KL(p||{p+q \over 2})+{1\over 2}KL(q||{p+q \over 2})\)
- 첫번째 텀: $E_{x \sim p_{data}(x)} \begin{bmatrix} log{2 \; * \; p_{data}(x) \over P_{data}(x) + p_g(x)}\end{bmatrix}$
두번째 텀: $E_{x \sim p_g(x)} \begin{bmatrix} log {2 \; * \; p_g(x) \over P_{data}(x) + p_g(x)} \end{bmatrix}$
JSD를 사용하기 위해 KL을 JSD형식으로 변환 \(= KL(p_{data} || {p_{data} + p_g (x) \over 2}) + KL(p_g||{p_{data}(x) + p_g(x) \over 2}) - log(4)\) \(C(G) = 2\; * \; JSD (p_{data} || p_g) - log(4)\)
- JSD 는 distance matric이기 때문에 최솟값이 0이며 이는 p와 q가 동일하다는 것을 뜻
- $p_{data}$ 와 $p_q$ 가 동일할 때 JSD는 0이되 사라져 최솟값으로 $-log(4)$ 를 얻을 수 있음
- Global Optimal Point를 얻을 수 있는 유일한 Solution은 생성자의 분포와 $p_{data}$가 동일할 때 즉 생성자가 내뱉는 이미지가 원본 데이터 distribution과 동일할 때 Global Optimal Point를 가질 수 있음
- 생성자는 매번 D가 이미 잘 수렴해서 Global Optimal을 가지고 있다고 가정한 상태에서 생성자가 잘 학습된다면 $-log(4)$ 를 가질 수 있도록 잘 수렴해서 $p_{data}$ 와 같은 분포를 가지는 형태로 수렴