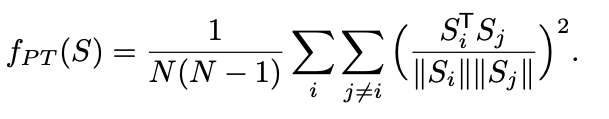12. EBGAN 이론 및 구현
Introduction
본 논문에서 제시하는 바는 Discriminator를 일종의 Energy Function으로 보자는것이다.
여기서 [Energy Function]이란, 데이터를 받았을 때 해당 데이터가 [Data Manifold]에 가까우면 낮은 값을 내놓고 Data Manifold에서 멀다면 높은 값을 내놓는 함수를 의미한다. 여기서 내놓는 값을 Energy 라고 한다.
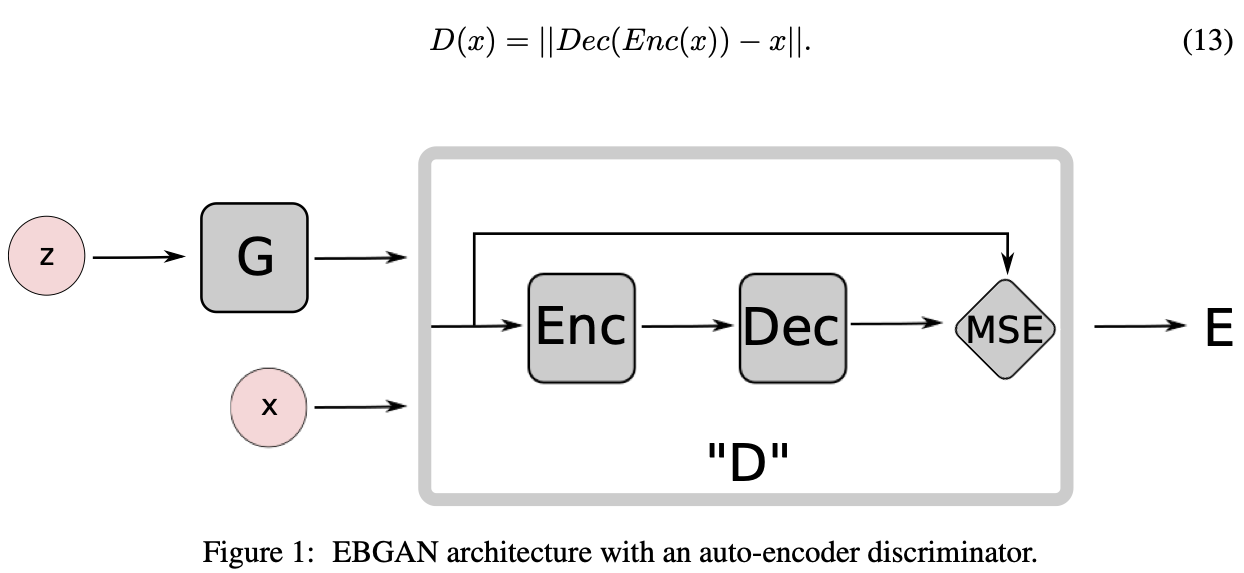
이와 같은 Energy Function 역할을 하는 Discriminator를 구성하기 위해 MSE Loss를 내놓는 Auto Encoder 구조를 제안한다.(real data에 가까우면 낮은 MSE를 내놓음 -> reconstruction을 잘한다)
EBGAN Model
Objective Functional
$(1)\;\;\;\;\;\;\;\;\;\;\;\;\;L_D(x, z) \; = \; D(x) + [m - D(G(z))]^+$ $(2)\;\;\;\;\;\;\;\;\;\;\;\;\; L_G(z) \; = \; D(G(z))$
Discriminator의 output은 Data Manifold에 가까울수록 작은 값을 내놓는 Energy 값이다. 그래서 Discriminator를 훈련시킬때 Fake Data에 대해서는 높은 값을 내놓도록 하고 Real Data에 대해서는 작은 값을 내놓도록 학습시켜야한다.
이런 Energy 기반 모델의 loss로 [margin loss]를 제안한다.
Optimality of the solution
논문에서 이 부분은 Vanila GAN 논문에서 제시한 것과 같이 이러한 방법이 Nash Equilibrium으로 이끈다는 것을 증명한다
Using Auto-Encoders
Discriminator가 Energy Function의 역할을 하기 위해서 Auto Encoder 형식과 MSE Loss를 output으로 내놓는 Architecture를 제안한다. (MSE Loss를 Energy로 보면 된다)
TMI
- 최근엔 Fast GAN이나 PatchGAN과 같이 Discriminator의 output이 단일 값이 아닌 경우가 존재하긴 하지만, 예전의 GAN 구조에서는 단일 값을 내놓는 형식이 흔한 구조
- 당시 상황에서 단일 값 (0 or 1)을 내놓는 standard GAN과 달리 모든 pixel을 비교하는 reconstruction based output은 다양한 direction의 gradient를 내놓을 수 있어서 더 큰 batch size를 사용할 수 있었다고 한다
Connection to the Regularized Auto-Encoders
오토인코더는 입력 데이터를 재구성하는 방식으로 훈련되는 신경망 모델이다. 그러나 오토인코더의 훈련에서 자주 발생하는 문제 중 하나는 모든 공간에서 입력 데이터를 완벽하게 재구성하는, 즉 완전한 항등 함수처럼 동작하는 경향이 있어서 데이터의 특징을 충분히 학습하지 못하는 경우이다. 이러한 문제를 피하기 위해서는 데이터 공간의 외부 영역에는 높은 에너지 값을 할당해야한다.
EBGAN은 이와 유사한 개념을 도입하여 훈련한다. 즉, EBGAN은 GAN 프레임워크이기 때문에 생성된 가짜 데이터에 대해 높은 에너지 값을 갖도록 훈련한다. 이렇게 함으로써 생성자를 일종의 정규화(regularization)로 간주할 수 있다.
이러한 접근 방식에서, 생성자는 생성된 가짜 데이터를 주어진 판별자에게 진짜 데이터로 오인하게끔 만들려고 노력합니다. 판별자는 진짜 데이터와 가짜 데이터를 구분하도록 최선을 다합니다. 따라서 생성자가 완벽하게 입력 데이터를 재구성하는 것을 피하고, 판별자가 데이터의 특징을 식별하는 데 도움이 되도록 에너지 값을 조정한다. 이와 같은 방식으로, EBGAN은 생성자를 정규화 메커니즘으로 활용하여 입력 데이터의 특징을 더욱 잘 포착할 수 있도록 돕는다.
Repelling Regularizer
본 논문에서는 Auto Encoder에 잘 어울리는 “Repelling Regularizer”를 제안한다.
Repelling Regularizer(또는 Repelling Loss)는 생성된 가짜 데이터가 서로 다른 특징을 갖도록 유도하는 정규화 기법이다. 이를 통해 생성자가 다양하고 다른 형태의 가짜 데이터를 생성하도록 돕는다.
Repelling Regularizer는 생성된 가짜 데이터 포인트 간의 거리를 증가시키는 방향으로 작동한다. 이는 가짜 데이터가 서로 가깝게 군집되는 것을 방지하고, 공간 전체에 걸쳐 더 분산되어 분포하도록 돕는 역할을 한다.
이를 수학적으로 표현하면, Repelling Regularizer는 가짜 데이터 포인트들 사이의 거리를 최대화하기 위해 데이터 포인트 쌍의 거리를 측정하고 해당 거리를 최소화하는 손실 함수를 추가한다. 이 손실 함수는 가짜 데이터 포인트 쌍의 거리 합을 최소화하는 방향으로 최적화된다.
Repelling Regularizer는 생성자의 출력 공간을 탐색하고 다양한 가짜 데이터를 생성하는 데 도움이 된다. 이를 통해 생성자는 다양한 형태와 특징을 갖는 가짜 데이터를 생성하여 더욱 다양하고 풍부한 데이터 분포를 모델링할 수 있다.
즉, Repelling Regularizer는 생성된 가짜 데이터의 다양성을 증가시키고, 훈련 데이터의 다양성과 비슷한 분포를 학습할 수 있도록 도와준다. 이는 생성자의 품질을 향상시키고 더 현실적이고 다양한 가짜 데이터를 생성할 수 있게 해준다.
두 가짜 데이터 포인트 $x_i$와 $x_j$ 사이의 거리를 $d(x_i, x_j)$ 로 나타내고 이 거리를 최소화하는 손실 함수로 Repelling Regularizer를 사용하게 되면 손실 함수는 다음과 같이 정의됩니다:
$L_{\text{repel}} = \frac{1}{N(N-1)} \sum_{i=1}^{N} \sum_{j\neq i}^{N} d(x_i, x_j)$
여기서 $N$ 은 가짜 데이터 포인트의 수
Repelling Regularizer의 값이 작아지면 가짜 데이터 포인트들 사이의 거리가 멀어지게 된다. 이를 통해 가짜 데이터 포인트들이 서로 멀리 떨어지도록 유도하여 분포의 다양성을 증가시킨다.
$d(x_i, x_j)$ 는 일반적으로 유클리디안 거리 또는 맨하탄 거리와 같은 거리 측정 방법을 사용하여 계산된다. 이 거리 함수는 데이터 포인트 사이의 유사성을 측정하는 척도로 사용된다.
따라서 Repelling Regularizer를 통해 생성자는 다양한 가짜 데이터를 생성하고, 가짜 데이터 포인트들이 서로 다른 형태와 특징을 갖도록 유도한다. 이는 생성자가 보다 다양한 데이터 분포를 모델링하고 훈련 데이터의 다양성을 따라갈 수 있도록 도와준다.
용어
- Data Manifold 데이터 공간에는 ‘데이터 매니폴드(Data Manifold)’라는 개념이 있습니다. 이는 고차원 데이터 공간에서 실제 데이터가 존재하는 저차원 부분공간을 의미합니다. 예를 들어, 모든 가능한 RGB 이미지를 생각해보면, 이들 중 실제로 유의미한 이미지는 그 공간의 매우 작은 부분에 위치하게 됩니다. 이렇게 데이터가 주로 존재하는 공간을 ‘데이터 매니폴드’라고 부릅니다.
- Energy Function 이 함수는 데이터 매니폴드에서의 각 점들이 얼마나 ‘자연스러운’ 데이터를 나타내는지를 측정하는 것으로 볼 수 있습니다. 이 함수는 주어진 데이터가 데이터 매니폴드에 가까울수록 낮은 값을, 매니폴드에서 멀수록 높은 값을 출력합니다. 즉, 이는 데이터의 ‘에너지’를 측정하는 것으로, 이 값이 낮다는 것은 그 데이터가 모델이 표현하려는 데이터 분포에 가깝다는 것을 의미합니다. 반대로, 에너지 값이 높다는 것은 그 데이터가 모델이 표현하려는 데이터 분포에서 멀리 떨어져 있다는 것을 의미합니다.
- Energy-based Model 에너지 기반 모델(Energy-based Model, EBM)은 이 에너지 함수를 최소화하는 방향으로 학습을 진행합니다. EBM에서의 학습 목표는 데이터의 에너지를 낮추고 (즉, 데이터 매니폴드에 가깝게 만드는 것), 또한 데이터 매니폴드 외부의 에너지를 높이는 것입니다. 이를 통해 모델은 실제 데이터 분포를 더 잘 표현할 수 있게 됩니다.
- Margin loss 판별자를 학습시키는 데 사용되는 특별한 손실 함수입니다. 이는 판별자가 실제 데이터와 생성된 데이터를 잘 구별할 수 있도록 돕습니다. 기본적으로, 마진 손실은 실제 데이터에 대한 에너지와 생성된 데이터에 대한 에너지 사이의 ‘마진’을 최대화하려는 목표를 가지고 있습니다. 이는 실제 데이터에 대한 에너지는 가능한 한 낮게 유지하면서, 동시에 생성된 데이터에 대한 에너지는 가능한 한 높게 유지하려는 것을 의미합니다. 수학적으로, 마진 손실은 다음과 같이 표현될 수 있습니다: $L = D(x) + max(0, m - D(G(z)))$ 여기서 D(x)는 실제 데이터 x에 대한 판별자의 출력(에너지)이고, D(G(z))는 생성된 데이터 G(z)에 대한 판별자의 출력입니다. m은 마진 파라미터로, 이 값은 실제 데이터와 생성된 데이터 사이의 에너지 차이에 대한 기대치를 설정합니다. 이 마진 손실 함수는 판별자가 실제 데이터와 생성된 데이터를 잘 구별하도록 돕는데, 실제 데이터에 대한 판별자의 에너지를 낮추고, 생성된 데이터에 대한 에너지를 높이는 방향으로 판별자를 학습시킵니다.
- Nash Equilibrium (내쉬 균형) 생성자와 판별자 간의 상호 작용에서 최적의 상태를 의미
EBGAN에서의 Nash 균형은 다음 조건을 만족하는 상태입니다.
- 생성자가 주어진 판별자에 대해 최적의 가짜 데이터를 생성하고,
- 판별자가 주어진 생성자에 대해 최적의 구분을 수행합니다. 즉, 생성자는 판별자가 가짜 데이터를 진짜로 오인하도록 최선의 노력을 기울이며, 판별자는 진짜 데이터와 가짜 데이터를 올바르게 구분하기 위해 최선을 다해야 합니다. 이러한 상황에서 생성자와 판별자는 더 이상 개선할 수 없는 최적의 상태에 도달하게 되고, 이것이 Nash 균형입니다. Nash 균형은 EBGAN에서 안정적인 학습을 도와주며, 생성자와 판별자 간의 균형을 유지하는 중요한 요소입니다.
EBGAN (Energy-Based Generative Adversarial Network)은 GAN(Generative Adversarial Networks)의 한 변형으로, 에너지 기반 모델(EBM: Energy-Based Model)의 개념을 도입하여 설계되었다. EBGAN의 목표는 에너지 함수를 최소화함으로써 실제 데이터 분포를 학습하는 것이다. 이 접근 방식에서, 판별자는 각 샘플에 대한 에너지를 할당하는 역할을 하며, 생성자는 낮은 에너지 값을 갖는 샘플을 생성하려고 한다다.
EBGAN의 핵심 개념
에너지 기반 모델(EBM): EBM은 데이터를 낮은 에너지로 매핑하려는 학습 모델이다. 실제 데이터 샘플은 낮은 에너지 값을 갖고, 비현실적인 데이터 샘플은 높은 에너지 값을 갖는다.
판별자(Discriminator)의 역할 변경: EBGAN에서 판별자는 전통적인 GAN에서처럼 진짜와 가짜를 구분하는 대신, 입력 샘플에 대한 에너지 점수를 계산한다. 낮은 에너지는 진짜 데이터와 유사함을, 높은 에너지는 가짜 데이터와 유사함을 나타낸다.
에너지 값의 의미
- 낮은 에너지 값: 실제 데이터 샘플과 유사한 샘플은 에너지 함수에 의해 낮은 에너지 값으로 평가된다. 낮은 에너지 값은 해당 샘플이 모델이 학습한 데이터 분포와 잘 일치함을 나타낸다. 즉, 모델은 실제 데이터 샘플을 “선호”하고, 이러한 샘플을 생성하려고 한다.
- 높은 에너지 값: 반면에, 비현실적이거나 실제 데이터 분포와 잘 일치하지 않는 샘플은 높은 에너지 값으로 평가된다. 높은 에너지 값은 해당 샘플이 모델에 의해 “불가능하거나” “덜 선호되는” 것으로 간주됨을 의미한다.
EBGAN의 손실 함수
EBGAN의 손실 함수는 두 부분으로 구성된다:
판별자 손실(Discriminator Loss):
\[L_D = D(x) + \max(0, m - D(G(z)))\]여기서 $D(x)$ 는 실제 데이터 $x$ 에 대한 판별자의 에너지 함수, $D(G(z))$ 는 생성된 데이터 $G(z)$ 에 대한 판별자의 에너지 함수, $m$ 은 마진(margin). 마진은 판별자가 실제 데이터와 생성된 데이터 사이에 유지하려는 에너지 간격을 나타낸다.
생성자 손실(Generator Loss):
$L_G = D(G(z))$
생성자의 목표는 판별자가 생성된 데이터에 낮은 에너지 값을 할당하도록 하는 것이다. 따라서 생성자 손실은 생성된 샘플의 에너지를 직접 최소화한다.
요약
EBGAN은 에너지 기반의 접근 방식을 GAN에 도입하여, 판별자가 데이터 샘플에 대한 에너지 점수를 계산하고, 생성자가 이 에너지를 최소화하도록 유도한다. 이는 전통적인 GAN과 비교했을 때, 학습의 안정성을 개선하고, 모델이 데이터의 다양한 특성을 더 잘 학습할 수 있도록 돕는다. EBGAN의 핵심은 판별자와 생성자 사이의 에너지 기반의 상호 작용을 통해, 실제 데이터 분포를 효과적으로 모델링하는 것이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import argparse
import os
import numpy as np
import math
import cv2
import matplotlib.pyplot as plt
import torchvision.transforms as transforms
from torchvision.utils import save_image
from torch.utils.data import DataLoader
from torchvision import datasets
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F
import torch
os.makedirs("images", exist_ok=True)
def weights_init_normal(m):
classname = m.__class__.__name__
if classname.find("Conv") != -1:
torch.nn.init.normal_(m.weight.data, 0.0, 0.02)
elif classname.find("BatchNorm") != -1:
torch.nn.init.normal_(m.weight.data, 1.0, 0.02)
torch.nn.init.constant_(m.bias.data, 0.0)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Option():
n_epochs = 200 # 학습을 수행할 에폭의 수
batch_size = 128 # 한 번에 학습할 배치의 크기
lr = 0.0002 # Adam 최적화기의 학습률
b1 = 0.5 # Adam 최적화기의 1차 모멘텀 감쇠율
b2 = 0.999 # Adam 최적화기의 2차 모멘텀 감쇠율
n_cpu = 8 # 배치 생성 시 사용할 CPU 스레드의 수
latent_dim = 62 # 잠재 공간의 차원 수
img_size = 32 # 각 이미지 차원의 크기
channels = 1 # 이미지 채널의 수
sample_interval = 200 # 이미지 샘플링 간격
opt = Option() # Option 클래스의 인스턴스 생성
# CUDA가 사용 가능한 경우 사용하도록 설정
cuda = True if torch.cuda.is_available() else False
# 이미지의 모양을 설정. (채널 수, 이미지 너비, 이미지 높이)의 형태로 설정된다.
img_shape = (opt.channels, opt.img_size, opt.img_size)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Generator(nn.Module):
def __init__(self):
# Generator 클래스를 nn.Module의 서브클래스로 초기화.
super(Generator, self).__init__()
# 초기 이미지 크기를 설정. 입력 이미지 크기의 1/4로 설정
self.init_size = opt.img_size // 4 # 8
# 첫 번째 레이어: 잠재 벡터(latent vector)를 받아 128 * 초기 이미지 크기의 제곱만큼의 뉴런을 가지는 선형 레이어
self.l1 = nn.Sequential(nn.Linear(opt.latent_dim, 128 * self.init_size ** 2)) # outputs = 128 * 64
# Convolutional block: 선형 레이어의 출력을 받아 이미지를 생성하는 컨볼루션 블록
self.conv_blocks = nn.Sequential(
# 이미지 크기를 2배로 업샘플링
nn.Upsample(scale_factor=2),
# 128개의 채널을 유지하면서 3x3 컨볼루션 적용
nn.Conv2d(128, 128, 3, stride=1, padding=1),
# 배치 정규화를 적용. 모멘텀: 0.8.
nn.BatchNorm2d(128, 0.8),
# LeakyReLU 활성화 함수를 적용. 음수 기울기는 0.2
nn.LeakyReLU(0.2, inplace=True),
# 다시 이미지 크기를 2배로 업샘플링
nn.Upsample(scale_factor=2),
# 64개의 채널로 차원을 축소하는 컨볼루션을 적용
nn.Conv2d(128, 64, 3, stride=1, padding=1),
# 배치 정규화를 적용
nn.BatchNorm2d(64, 0.8),
# LeakyReLU 활성화 함수를 적용
nn.LeakyReLU(0.2, inplace=True),
# 최종 채널 수로 차원을 맞추는 컨볼루션을 적용
nn.Conv2d(64, opt.channels, 3, stride=1, padding=1),
# Tanh 활성화 함수를 적용하여 출력을 [-1, 1] 범위로 조정
nn.Tanh(),
)
def forward(self, noise):
# 잠재 벡터를 첫 번째 레이어에 통과
out = self.l1(noise)
# 출력을 적절한 형태로 재구성
out = out.view(out.shape[0], 128, self.init_size, self.init_size) # (배치 ,in_channel: 128, 8, 8)
# 컨볼루션 블록을 통과시켜 최종 이미지를 생성
img = self.conv_blocks(out)
return img
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Discriminator(nn.Module):
def __init__(self):
# Discriminator 클래스를 nn.Module의 서브클래스로 초기화
super(Discriminator, self).__init__()
# 첫 번째 컨볼루션 레이어: 이미지를 입력으로 받아 크기를 줄임
self.down = nn.Sequential(nn.Conv2d(opt.channels, 64, 3, 2, 1), nn.ReLU())
# 다운샘플링 후의 이미지 크기 설정
self.down_size = opt.img_size // 2 # 16
# 다운샘플링 후의 차원 계산
down_dim = 64 * (opt.img_size // 2) ** 2 # 64 * 16 * 16
# Embedding layer: 다운샘플링된 이미지를 임베딩하는 선형 레이어.
self.embedding = nn.Linear(down_dim, 32)
# Fully-connected layers: 임베딩된 벡터를 처리하는 완전 연결 레이어.
self.fc = nn.Sequential(
nn.BatchNorm1d(32, 0.8),
nn.ReLU(inplace=True),
nn.Linear(32, down_dim),
nn.BatchNorm1d(down_dim),
nn.ReLU(inplace=True),
)
# Upsampling: 완전 연결 레이어의 출력을 업샘플링하여 최종 이미지 크기로 조정. (오토 인코더 구조)
self.up = nn.Sequential(nn.Upsample(scale_factor=2), nn.Conv2d(64, opt.channels, 3, 1, 1))
def forward(self, img):
# 입력 이미지를 다운샘플링.
out = self.down(img)
# 이미지를 임베딩.
embedding = self.embedding(out.view(out.size(0), -1))
# 완전 연결 레이어를 통과
out = self.fc(embedding)
# 업샘플링하여 최종 출력 생성
out = self.up(out.view(out.size(0), 64, self.down_size, self.down_size))
# 최종 출력과 임베딩된 벡터를 반환
return out, embedding
EBGAN(Energy-based Generative Adversarial Networks)과 같은 생성 모델에서 다운 샘플링된 이미지를 임베딩하는 과정은 여러 가지 목적과 장점을 가지고 있다. 임베딩은 고차원 데이터를 저차원의 밀집 벡터로 변환하는 과정을 의미한다. 이러한 변환을 통해, 모델은 데이터의 중요한 특성을 보다 효율적으로 학습하고, 노이즈를 줄이며, 계산 비용을 감소시킬 수 있다.
Seq2Seq 모델에서의 임베딩
- 비슷한 의미를 가진 단어의 밀집: Seq2Seq 모델에서 단어 임베딩은 비슷한 의미를 가진 단어들이 임베딩 공간에서 서로 가깝게 위치하도록 만든다. 이를 통해 모델은 단어 간의 의미적 유사성을 학습하고, 이를 기반으로 텍스트를 처리한다.
- 차원 축소: 단어 임베딩은 자연어를 다룰 때 발생하는 고차원의 문제(예: 단어의 원-핫 인코딩)를 저차원의 연속 벡터로 변환한다. 이 저차원의 벡터는 단어의 의미를 효과적으로 포착할 수 있으며, 계산 효율성을 높힌다.
GAN 또는 EBGAN에서의 이미지 임베딩
- 비슷한 이미지 분포의 밀집: 이미지 데이터를 처리할 때, 임베딩은 비슷한 특성이나 패턴을 가진 이미지들이 임베딩 공간에서 서로 가까이 위치하도록 한다. 이를 통해 모델은 이미지 간의 유사성과 차이를 더 잘 이해하고, 이를 기반으로 이미지를 생성하거나 변환할 수 있다.
- 차원 축소와 정보의 밀도 증가: 이미지 임베딩은 고차원의 이미지 데이터를 저차원의 벡터로 압축하여 표현한다. 이 과정에서 중요한 정보를 보존하면서 데이터를 더 효율적으로 처리할 수 있다. 또한, 저차원의 임베딩 공간에서는 데이터의 내재적인 구조와 패턴을 더 명확하게 학습할 수 있다.
임베딩을 통한 학습 효율성과 성능 향상
임베딩을 사용함으로써, 모델은 비슷한 데이터 포인트들을 임베딩 공간에서 서로 가깝게 배치함으로써 데이터의 복잡성을 관리하고, 학습 과정에서 데이터 간의 관계를 더 잘 이해할 수 있다. 이는 학습의 효율성을 높이고, 모델의 성능을 개선하는 데 도움이 됩니다. 또한, 임베딩은 모델이 데이터의 추상적인 특성과 구조를 학습하는 데 중요한 역할을 하며, 이를 통해 보다 복잡하고 다양한 데이터 처리 작업을 수행할 수 있게 된다.
임베딩의 장점
- 차원 축소: 고차원 이미지 데이터를 저차원으로 변환함으로써, 데이터의 핵심적인 특성을 보존하면서도 차원의 저주를 완화할 수 있다. 이는 모델이 학습하기 더 쉬운 데이터 표현을 제공한다.
- 학습 효율성 증가: 저차원 임베딩은 모델이 필요한 정보를 더 적은 양의 데이터로부터 추출할 수 있도록 한다. 이는 학습 과정에서의 메모리 사용량과 계산 비용을 줄이는 데 도움된다.
- 노이즈 감소: 다운 샘플링과 임베딩 과정은 불필요한 정보나 노이즈를 제거하는 효과가 있어, 모델이 데이터의 중요한 특징에 더 집중할 수 있게 함
- 일반화 능력 향상: 임베딩을 통해 추출된 저차원 표현은 모델이 학습 데이터에 과적합되는 것을 방지하고, 일반화 능력을 향상시킬 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# Reconstruction loss of AE
pixelwise_loss = nn.MSELoss() # 픽셀 단위의 손실 함수를 평균 제곱 오차(MSE)로 설정
# Initialize generator and discriminator
generator = Generator() # 생성자 인스턴스 생성
discriminator = Discriminator() # 판별자 인스턴스 생성
# CUDA 사용 가능 여부에 따라 모델과 손실 함수를 GPU로 이동
if cuda:
generator.cuda()
discriminator.cuda()
pixelwise_loss.cuda()
# 모델의 가중치 초기화
generator.apply(weights_init_normal)
discriminator.apply(weights_init_normal)
# 데이터 로더 설정
os.makedirs("dataset/mnist", exist_ok=True) # 데이터셋을 저장할 디렉토리 생성
dataloader = torch.utils.data.DataLoader(
datasets.MNIST(
"dataset/mnist", # 데이터셋 경로
train=True, # 훈련 데이터셋 사용
download=False, # 데이터셋을 다운로드하지 않음
transform=transforms.Compose([ # 이미지 전처리
transforms.Resize(opt.img_size), # 이미지 크기 조정
transforms.ToTensor(), # 이미지를 텐서로 변환
transforms.Normalize([0.5], [0.5]) # 정규화
]),
),
batch_size=opt.batch_size, # 배치 크기 설정
shuffle=True, # 데이터셋을 무작위로 섞음
)
# 최적화 함수 설정
optimizer_G = torch.optim.Adam(generator.parameters(), lr=opt.lr, betas=(opt.b1, opt.b2))
optimizer_D = torch.optim.Adam(discriminator.parameters(), lr=opt.lr, betas=(opt.b1, opt.b2))
# CUDA 사용 여부에 따라 적절한 텐서 타입 설정
Tensor = torch.cuda.FloatTensor if cuda else torch.FloatTensor
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# Pull away loss 함수 정의
def pullaway_loss(embeddings):
"""
생성된 샘플들 간의 다양성을 증가시키기 위한 Pull away loss 계산
Args:
embeddings: 생성자로부터 생성된 샘플들의 특성 임베딩
Returns:
loss_pt: Pull away loss 값
"""
# 각 임베딩의 노름(norm) 계산
norm = torch.sqrt(torch.sum(embeddings ** 2, -1, keepdim=True))
# 임베딩을 정규화
normalized_emb = embeddings / norm
# 정규화된 임베딩 간의 유사도 계산
similarity = torch.matmul(normalized_emb, normalized_emb.transpose(1, 0)) # 전치
batch_size = embeddings.size(0) # 배치 크기
# 유사도 행렬에서 대각선을 제외한 모든 요소의 합을 계산하고, 이를 통해 pull away loss 계산
loss_pt = (torch.sum(similarity) - batch_size) / (batch_size * (batch_size - 1))ㅌ
"""
'pull away loss'는 생성된 샘플들의 임베딩 벡터가 서로 다를수록 (즉, 유사도가 낮을수록) 손실이 감소하도록 설계되어 있어,
생성자가 다양한 샘플을 생성하도록 유도. 이는 생성된 이미지들이 서로 닮지 않게 하여, 모델의 다양성을 향상시키는 데 도움 된다.
"""
return loss_pt
1. 단위 길이(Unit Length)란?
단위 길이를 갖는다는 것은, 벡터의 길이(또는 크기)가 1이라는 의미. 여기서 길이나 크기는 벡터의 모든 요소의 제곱 합의 제곱근으로 계산된다, 즉 $L2$ 노름이라고도 한다.
벡터 $\mathbf{v}$의 $L2$ 노름(길이) 계산: \(\|\mathbf{v}\| = \sqrt{v_1^2 + v_2^2 + \dots + v_n^2}\) 여기서 $v_1, v_2, \dots, v_n$은 벡터의 각 요소
벡터를 단위 길이로 정규화하는 과정은, 원래 벡터를 그의 $L2$ 노름으로 나누어 수행: \(\mathbf{v}_{\text{normalized}} = \frac{\mathbf{v}}{\|\mathbf{v}\|}\) 이렇게 정규화된 벡터는 방향은 유지하면서 길이가 1이 된다. 이는 유사도 계산 시 벡터의 방향성은 중요하지만 크기는 중요하지 않을 때 유용하다.
2. 내적과 코사인 유사도의 관계
벡터 간의 내적(dot product)과 코사인 유사도는 밀접하게 연관되어 있다. 코사인 유사도는 두 벡터 간의 각도를 기반으로 유사성을 측정하는 방법으로, 벡터의 방향이 얼마나 유사한지를 나타낸다.
코사인 유사도 정의: \(\text{cosine similarity}(\mathbf{a}, \mathbf{b}) = \frac{\mathbf{a} \cdot \mathbf{b}}{\|\mathbf{a}\| \|\mathbf{b}\|}\)
여기서 $\mathbf{a} \cdot \mathbf{b}$ 는 두 벡터의 내적이고, $|\mathbf{a}|$와 $|\mathbf{b}|$는 각각 벡터 $\mathbf{a}$와 $\mathbf{b}$의 $L2$ 노름
두 벡터가 모두 단위 길이로 정규화되어 있다면, 즉 $|\mathbf{a}| = |\mathbf{b}| = 1$ 이라면, 코사인 유사도는 단순히 두 벡터의 내적과 같아진다:
\[\text{cosine similarity}(\mathbf{a}, \mathbf{b}) = \mathbf{a} \cdot \mathbf{b}\]이는 정규화된 벡터들의 내적을 사용하여 직접 코사인 유사도를 계산할 수 있음을 의미한다. 따라서, 내적은 정규화된 벡터들 사이의 유사도를 계산하는 간편하고 효율적인 방법을 제공한다.
- 임베딩의 크기 계산:
norm = torch.sqrt(torch.sum(embeddings ** 2, -1, keepdim=True))이 부분에서는 각 임베딩 벡터의 L2 노름(크기)을 계산. 여기서embeddings ** 2는 벡터의 각 요소를 제곱하고,torch.sum(..., -1, keepdim=True)는 각 임베딩에 대해 모든 차원을 합산하여 그 크기를 구한 다음, 제곱근을 취함으로써 최종적으로 각 임베딩 벡터의 노름을 구한다.
- 임베딩 정규화:
normalized_emb = embeddings / norm이 부분에서는 각 임베딩 벡터를 그의 노름으로 나누어 정규화 한다. 이렇게 함으로써, 각 임베딩 벡터는 단위 길이를 갖게 되며, 이는 유사도 계산 시 벡터의 크기가 결과에 영향을 주지 않도록 한다.
- 유사도 계산:
similarity = torch.matmul(normalized_emb, normalized_emb.transpose(1, 0))이 부분에서는 정규화된 임베딩 벡터 간의 코사인 유사도를 계산한다. 내적(dot product)을 사용하여 정규화된 벡터들 간의 유사도를 계산하고, 이는 각 벡터 쌍 간의 유사성을 나타내는 행렬을 생성한다.
- 손실 계산:
loss_pt = (torch.sum(similarity) - batch_size) / (batch_size * (batch_size - 1))이 부분에서는 계산된 유사도 행렬을 사용하여 pull-away loss를 계산한다. 여기서torch.sum(similarity) - batch_size는 자기 자신과의 유사도(자기 자신과의 유사도는 1)를 제외한 모든 유사도 값들의 합을 계산한다. 그 후, 이 값을(batch_size * (batch_size - 1))으로 나누어 평균을 구한다. 이는 각 임베딩 벡터가 다른 모든 벡터와 얼마나 다른지를 측정하며, 이 값이 작을수록 각 임베딩이 서로 다른 방향을 가리키고 있음을 의미한다.
즉, 이 함수는 임베딩 벡터들이 서로 다른 특성을 가지고 있도록 격려함으로써, 모델이 더 다양한 특성을 학습하게 하려는 목적으로 사용된다. 이는 특히 생성 모델에서 각 샘플이 서로 다른 특성을 가지도록 하여 다양성을 증가시키는 데 유용하다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
# EBGAN에 사용될 하이퍼파라미터 설정
lambda_pt = 0.1 # Pull away loss의 가중치
margin = max(1, opt.batch_size / 64.0) # 판별자 손실 함수에서 사용될 마진 값 설정
for epoch in range(opt.n_epochs):
for i, (imgs, _) in enumerate(dataloader):
# 실제 이미지를 적절한 텐서로 변환
real_imgs = Variable(imgs.type(Tensor))
# -----------------
# Train Generator
# -----------------
optimizer_G.zero_grad() # 생성자의 그래디언트를 초기화
# 잠재 공간에서 노이즈 샘플링
z = Variable(Tensor(np.random.normal(0, 1, (imgs.shape[0], opt.latent_dim))))
# 노이즈로부터 이미지 생성
gen_imgs = generator(z)
# 생성된 이미지를 판별자에 통과시켜 재구성 이미지와 임베딩을 얻음
recon_imgs, img_embeddings = discriminator(gen_imgs)
# 생성자 손실 계산: 재구성 손실 + pull away loss
g_loss = pixelwise_loss(recon_imgs, gen_imgs.detach()) + lambda_pt * pullaway_loss(img_embeddings)
g_loss.backward() # 손실에 대해 역전파 실행
optimizer_G.step() # 생성자의 가중치 업데이트
# ---------------------
# Train Discriminator
# ---------------------
optimizer_D.zero_grad() # 판별자의 그래디언트를 초기화
# 실제 이미지와 생성된 이미지를 판별자에 통과시켜 재구성 손실 계산
real_recon, _ = discriminator(real_imgs)
fake_recon, _ = discriminator(gen_imgs.detach())
d_loss_real = pixelwise_loss(real_recon, real_imgs) # 실제 이미지의 재구성 손실
d_loss_fake = pixelwise_loss(fake_recon, gen_imgs.detach()) # 생성된 이미지의 재구성 손실
# 판별자 손실 계산: 실제 이미지의 재구성 손실 + 가짜 이미지의 재구성 손실(마진 적용)
"""
이게 맞는 설명인지는 모르겠으나 일단...
로스가 마진보다 크다는건 이미 학습에 어려움을 겪고 있으므로 놔두는거고,
마진보다 작으면 더 학습할 수 있는 여지가 있어서 패널티를 준다
"""
d_loss = d_loss_real
if (margin - d_loss_fake.data).item() > 0:
d_loss += margin - d_loss_fake
d_loss.backward() # 손실에 대해 역전파 실행
optimizer_D.step() # 판별자의 가중치 업데이트
# 주기적으로 학습 상태 출력 및 생성된 이미지 저장
batches_done = epoch * len(dataloader) + i
if batches_done % opt.sample_interval == 0:
print("[Epoch %d/%d] [Batch %d/%d] [D loss: %f] [G loss: %f]"
% (epoch, opt.n_epochs, i, len(dataloader), d_loss.item(), g_loss.item()))
save_image(gen_imgs.data[:25], "images/%d.png" % batches_done, nrow=5, normalize=True)
plt.figure(figsize = (5,5))
img1 = cv2.imread("images/%d.png" %batches_done)
plt.imshow(img1, interpolation='nearest')
plt.axis('off')
plt.show()