Post

Dropout 논문 리뷰

Posted
By JUNHEE LEE
13 min read
태그#Training
한줄요약Dropout
Journal/Conference#JMLR
LinkDropout
Year(출판년도)2014
저자N Srivastava, G Hinton, A Krizhevsky, I Sutskever, R Salakhutdinov
원문 링크Dropout




핵심 요약

  • Deep Neural Network 의 Regularization 방법인 Dropout 을 제시한 논문.
  • 학습 과정에서 일부 Node 를 제외(Drop)하는 것 만으로 Overfitting 을 방지할 수 있는 단순한 방법을 제시.




Introduction

Dropout 이전에도 overfitting 을 해결하기 위한 다양한 방법이 제시되어 왔다.

  • Early Stopping : validation accuracy가 증가하지 않을 때까지 학습
  • L1/L2 정규화(regularization)
  • soft weight sharing

논문은 가능한 모든 파라미터의 조합에서 생성된 예측을 학습 데이터의 사후 확률로 가중 평균하였을 때, Bayesian Gold Standard 라 부르는 최고의 정규화 성능을 이룰 수 있다고 말한다. 그러나 이는 크기가 작고 파라미터 수가 적은 모델이 아닌 경우 적용하기 어렵다.

모델을 일반화하기 위한 또다른 방법으로는 Model Combination 이 존재한다. 구조가 다른 모델이나, 훈련 데이터가 다른 여러 모델의 결과를 종합하는 해당 방법은, 당연하게도 많은 연산량과 학습 시간을 요구한다.

Dropout 은 신경망을 구성하는 각각의 뉴런을 확률적으로 제외하는 것만으로도, 과적합 해결 및 Model Combination 의 비효율성을 해결할 수 있음을 제시한다.

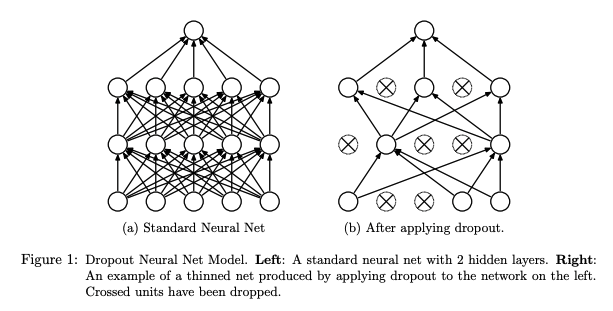
(a)와 같이 n 개의 뉴런으로 이루어진 신경망 각각에 Dropout 을 적용한다면, (b)와 같은 subnet을 2^n 개 얻을 수 있다. 훈련과정에서 이러한 Dropout 을 수행함으로서, 2^n 개의 신경망을 동시에 학습하는 것과 같은 결과를 얻을 수 있게 된다.

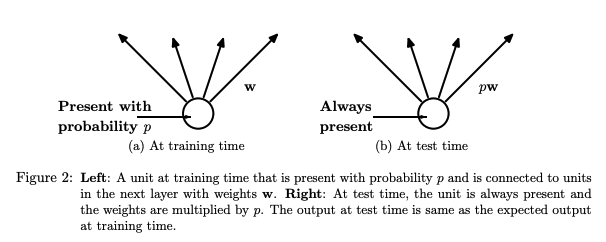
훈련이 끝나고 모델을 테스트하는 경우에는 모델 구조를 고정해서 사용해야 한다. 이를 위해, Dropout 을 수행한 뉴론의 가중치에, Dropout 확률을 곱하여 사용한다. 이 방법으로, 훈련 시기 뉴런의 expected output과 테스트 시기 뉴런의 output 을 일치시킬 수 있다.




Motivation

Dropout 의 아이디어는 유성 생식에서 출발한다. 무성 생식보다 복잡한 유성 생식이 우세한 이유에 대해, 유전 정보를 랜덤하게 섞어 생식을 수행하는 과정에서 유전자가 어떠한 경우에도 원활하게 작동하도록 Robust 하게 진화되었음을 주장한다. Dropout 또한 학습 과정에서 뉴런이 스스로 Robust 해질 수 있도록 설계한 방법이다.




Model description

다음의 표기를 사용하여 모델을 설명

  • $L$ : hidden layer 갯수
  • $l$ : 임의의 hidden layer
  • $z^{(l)}$ : $l$ 번째 layer 의 input vector
  • $y^{(l)}$ : $l$ 번째 layer 의 output vector
  • $W^{(l)}$ : $l$ 번째 layer 의 Weight
  • $b^{(l)}$ : $l$ 번째 layer 의 bias
  • $f$ : 활성 함수(activation function) : sigmoid, ReLU 등

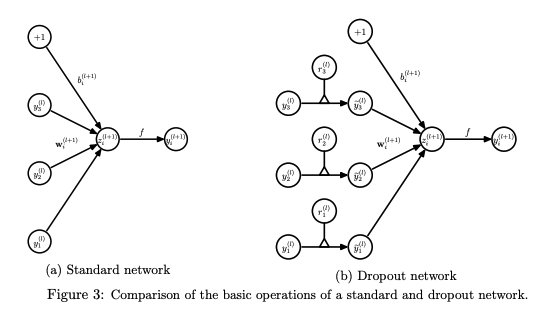
이 때, Dropout 이 포함된 Feed Forward operation 은 아래와 같다.

\[\begin{align*} r_j^{(l)} & \approx \text{Bernoulli}(p), \\ \tilde{\bf{y}}^{(l)} & = \mathbf{r}^{(l)} \ast \mathbf{y}^{(l)}, \\ z_i^{(l+1)} & = \mathbf{w}_i^{(i+1)} \tilde{\bf{y}}^l + b_i^{(l+1)}, \\ y_i^{(l+1)} & = f( z_i^{(l+1)}).\\ \end{align*}\]

$\text{Bernoulli}(p)$는 베르누이 이항 분포로, Dropout node 가 $p$ 의 확률로 켜짐을 의미한다.

앞서 언급했듯, Test시에는 dropout을 사용하지 않고 weight에 확률 p 를 곱하여 사용한다.




Learning Dropout Nets

Backpropagation

일반적인 신경망과 같이 SGD 를 사용한다. 단, mini batch 에서 thinned network 를 구성하는 요소에만 SGD 를 적용하며, 이 과정에서 gradient 가 평균화된다.

또한 SGD를 보완하기 위한 방법들인 momentum, annealed learning rate, L2 weight decay 등을 dropout 신경망에서 사용할 때도 좋은 결과를 보였음을 제시한다.

논문은 특히 max norm regularization 이 가장 좋은 효과를 보였다고 한다. max norm 을 제한된 크기의 가중치 구슬이 가중치 공간을 탐색하는 것으로 비유하며, Dropout 이 가중치 공간에 노이즈를 주어 더 많은 가중치 공간을 빠르게 탐색하는데 도움을 줄 수 있음을 제시한다.




Experimental Results

위와 같이 이미지, 음성, 자연어 등 다양한 데이터셋을 위한 인공 신경망에 Dropout 을 적용한 결과를 제시한다.

구조에 관계없이 Dropout 의 적용 여부 만으로 Test Error 가 확연하게 감소한 결과를 제시한다.

또한, 다른 Regularization 방법에 비해서도 우수한 성능을 보임을 제시한다. ReLU 활성 함수를 사용하고 SGD 로 학습하는 동일한 네트워크에서 Regularization 만을 다르게 수행하였을 때, Dropout 을 적용한 경우에 가장 적은 에러를 보인다.




Salient Features

Dropout 이 신경망에 미치는 다양한 영향을 분석한 결과를 제시한다.



Effect on Features

인공신경망의 가중치를 업데이트하는 과정에서 뉴런은 다른 뉴런의 영향이 주어진 상황에서 최적화를 진행한다. 이렇게 여러 뉴런이 co-adaptation 되는 경우에 신경망은 데이터를 일반화하지 못하고 과적합을 발생시킨다.

  • (a)는 feature 가 뚜렷하게 관측되지 않고 co-adaptation 이 발생했음을 보인다.
  • (b)는 dropout 을 통해 co-adaptation 을 억제하여, 가장자리/선 등 의미있는 feature 를 추출했음을 보인다.



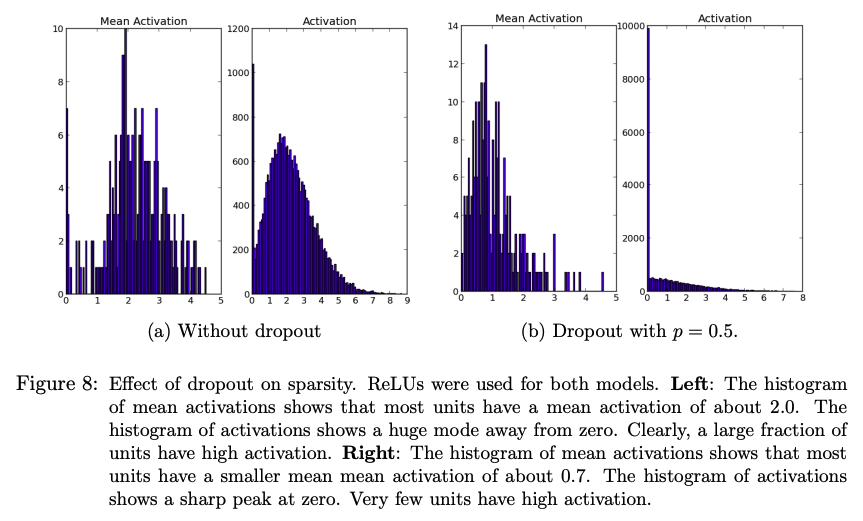
Effect on Sparsity

Dropout 은 hidden unit 의 activation 을 대부분 0으로 만들어 sparse 하게 만든다. activation 이 0에 가깝고 high activation 의 비율이 낮은 경우 모델은 더 좋은 성능을 보인다.

  • (a) Dropout 미적용시 activation 평균은 2.0이고, 0이 아닌 high activation 이 다수 존재한다.
  • (b) Dropout 을 적용할 시 activation 의 평균은 0.7 로 0에 가까워졌고, 대부분 0으로 activation 된다.



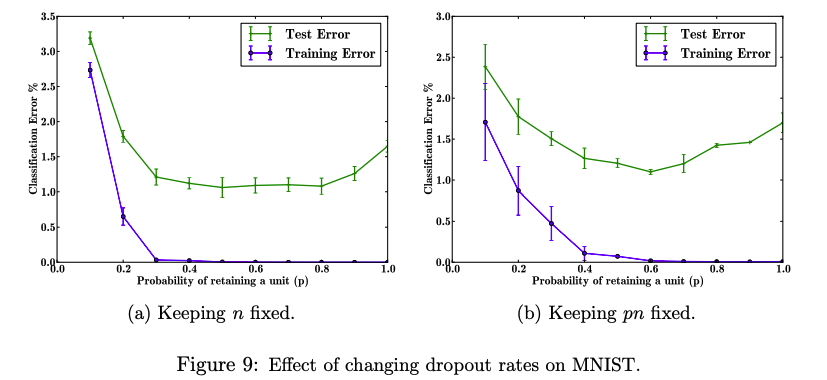
Effect on Dropout Rate

Dropout rate p 는 hyperparameter 로 유저에 의해 조정된다. 최적의 p 를 테스트하기 위해 진행한 실험과 결과를 제시한다.

  • (a) hidden layer 의 뉴런 수 $n$ 을 고정한 경우
    • p가 증가할수록 Test Error가 감소한다.
    • $0.4 ≤ p ≤ 0.8$ 범위에서는 비슷한 Test Error를 보이며 더 효과가 좋아지지는 않았다.
    • 그 이상에서는 Underfitting 으로 예상되는 Test Error 증가를 보인다.
  • (b) $np$ 를 고정
    • 낮은 p 에서 $n$ 이 늘어나면서, $n$ 을 고정했을 때 보다 더 낮은 Test Error 를 보인다.
    • 0.6 에서 가장 낮은 Test Error 를 보인다.

종합했을 때 약 0.6이 최적의 p 이지만, 논문은 편의를 위해 최적에 가까운 0.5 를 사용하는 것을 제안한다.



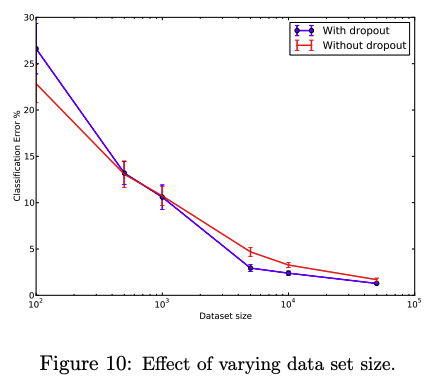
Effect of Data Set Size

1000개 이하의 적은 데이터로는 Dropout 이 유의미한 결과를 보이지 못한다. 이외에도 데이터셋의 크기가 커질 수록 Overfitting 의 가능성이 낮아지므로, Dropout 의 효과 또한 감소하는 것을 확인할 수 있다.



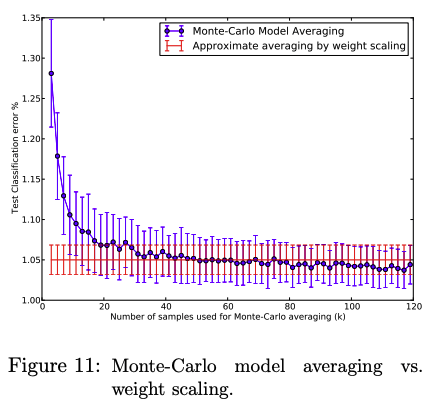
Monte-Carlo Model Averaging vs. Weight Scaling

논문은 Test 상황에서도 Dropout 을 수행한 여러 결과를 얻어낸 뒤 이를 평균낸 것이 True modeling 에 가깝다고 말한다. 이를 증명하기 위해, 서로 다른 Dropout 을 수행한 $k$ 개의 모델 출력을 종합한 Monte-Carlo 평균 결과와, weight 를 dropout rate 로 scaling 한 모델의 결과를 비교하여 제시한다. $k$ 의 갯수가 작으면 평균의 효과를 충분히 보지 못하여 오히려 큰 에러를 보이고, 충분히 큰 k 가 되었을 때에도 weight scaling 과 비슷한 결과를 보인다.




Dropout RBM

Dropout 을 Feed-forward 신경망이 아닌 랜덤 볼츠만 머신(RBM)에 적용하였을 때도, 더 선명한 Feature 와 좋은 일반화 성능을 보임을 제시한다.




Marginalizing Dropout

Dropout 은 신경망의 hidden unit 에 노이즈를 추가하는 것으로 볼 수 있습니다. 따라서, Dropout 을 사용한 모델은 stochastic 한 성질을 보인다. 논문은 이러한 노이즈를 marginalize 하여 dropout 을 deterministic 하게 모델링하는 방법을 제시한다. 이를 통해, 가장 간단한 Linear Regression 에서 Dropout 은 L2 Regularization 을 수행한 것과 동일하다는 결과를 보인다.




Conclusion

Dropout 은 신경망을 구성하는 노드를 임의로 학습에 제거하는 방법만으로 과적합을 방지한다. 이는 Co-adaptation 을 방지하며 Feature 를 선명하게 만들어준다. 이러한 Dropout 은 논문 당시 기준으로 SVHN, ImageNet, CIFAR-100, MNIST 데이터셋에서 State-of-the-art 를 달성하였다. 반면 Dropout 으로 인하여 학습 시간이 증가할 수도 있음을 제시하지만, 잡음을 통해서 오히려 신경망을 강건하게 만들어 줄 수 있음을 제시한다. 이후 Dropout 은 Tensorflow, Keras, Pytorch 등의 딥러닝 라이브러리 등에서 필수적으로 포함된 중요한 기법이 되었다.

논문 리뷰, Training
Training Dropout
This post is licensed under CC BY 4.0 by the author.