3. DCGAN 이론 및 구현

</br>

요약

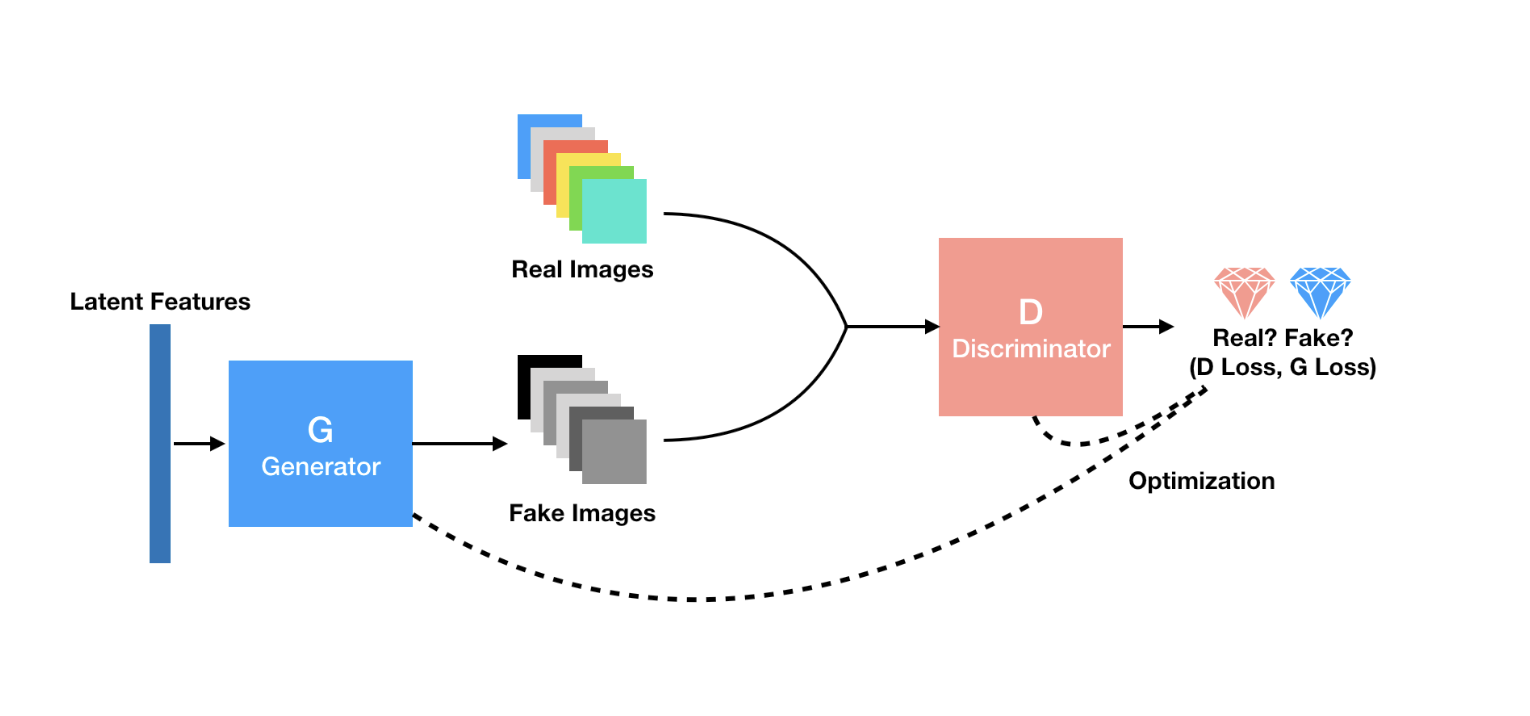
DCGAN은 GAN의 개선 모델로 GAN과 다른 점은 다음과 같다

• D(Discriminator)
  • Strided Convolution을 사용
  • Batch Normalization을 사용. 입력 레이어 (첫번째)에는 사용하지 않는다
  • activation function으로 Leaky ReLU를 사용
• G(Generator)
  • Fractional Strided Convolution(Transposed Convolution)을 사용
  • Batch Normalization을 사용. 출력 레이어(마지막)에는 사용하지 않는다.
  • activation function으로 ReLU를 사용하고 마지막 레이어는 tanh를 사용

$\star$논문에서 deconvolution이라 되어 있는 것은 Transposed 또는 fractional strided convolution을 의미. 이 연산은 convolution의 역연산이 아님

</br> </br>

GAN Review

</br> </br>

기존 GAN의 한계

1. GAN의 결과가 불안정하다
   • 기존 GAN만 으로는 성능이 잘 나오지 않았다
2. Black-box method
   • Neural Network 자체의 한계라고 볼 수 있는데, 결정 변수나 주요 변수를 알 수 있는 다수의 머신러닝 기법들과 달리 Neural Network는 처음부터 끝까지 어떤 형태로 그러한 결과가 나오게 되었는지 그 과정을 알 수 없다.
3. Generative Model 평가
   • GAN은 결과물 자체가 새롭게 만들어진 Sample이다. 이를 기존 sample과 비교하여 얼마나 비슷한지 확인할 수 있는 정략적 척도가 없고, 사람이 판단하더라도 이는 주관적인 기준이기 때문에 얼마나 정확한지, 혹은 뛰어난지 판단하기 힘들다

</br> </br>

DCGAN의 목표

1. Generator가 단순 기억으로 generate하지 않는다는 것을 보여줘야 한다.
2. z(sampling 된 noise vector) 의 미세한 변동에 따른 generator 결과가 연속적으로 부드럽게 이어져야 한다. (이를 walking in the latent space라고 한다.)

</br> </br>

Architecture Guidelines

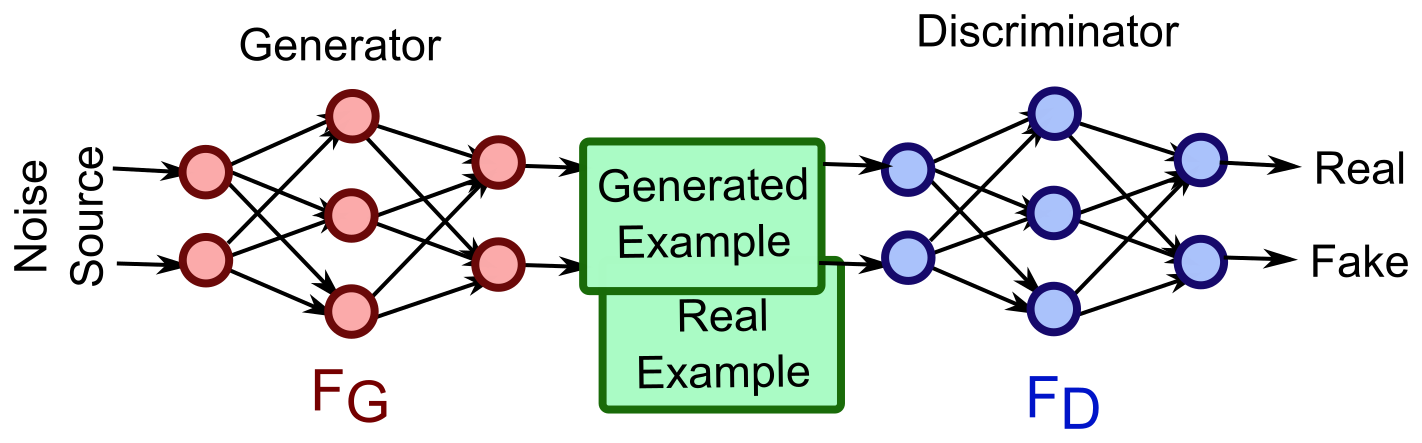
GAN과 DCGAN의 전체적인 구조는 거의 유사. 다만 각각의 Discriminator와 Generator의 세부적인 구조가 달라진다.

논문발췌

GAN에 CNN을 써서 이미지 품질을 높이려는 시도는 지금까지 성공적이지 못했다.

우리는 많은 시도 끝에 다양한 데이터셋에서 안정적인 그리고 더 높은 해성도의 이미지를 생성하는 모델 구조를 찾아내었다. 핵심은 다음 3가지를 CNN구조에 적용시키는 것이다.

1. max-pooling 과 같은 미분불가능한 레이어를 strided convolution으로 바꿔 
	spatial downsampling이 가능하게 한 것이다. 이는 G에 사용된 것이고, D에는 
	unsampling 이 가능하게 바꿨다

2. 요즘 트랜드는 FC(Fully Connected) Layer를 없애고 convolution layer로 바꾸는 것.

3. Batch Normalization을 사용하여 학습을 안정화시킨다
	(*2019년 현재 BN은 거의 필수처럼 되어 있다.) 
	이는 weight 초기화가 나쁘게 된 경우와 깊은 모델에서 gradient flow를 도우며,
	이는 학습 초기에 잘못된 방향으로 학습이 진행되어 망해가는 경우를 막아준다.

	그러나 sample이 요동치는 것을 막기 위해 G의 출력 레어이어와 D의 input layer에 
	는 넣지 않았다.(수많은 시도 끝에 알아냄)


G에서는 activation function으로 ReLU를 사용하고 마지막 레이어에는 tanh를 사용한다. Bounded activation(tanh)은 더 빠르게 수렴하고 학습샘플의 분포를 따라갔다. 
D에는 Leaky ReLU를 사용하여 높은 해상도를 만들 수 있게 하였다. 

이는 GAN과 다른 부분이다. 

</br> </br>

기존 GAN Architecture

</br> </br>

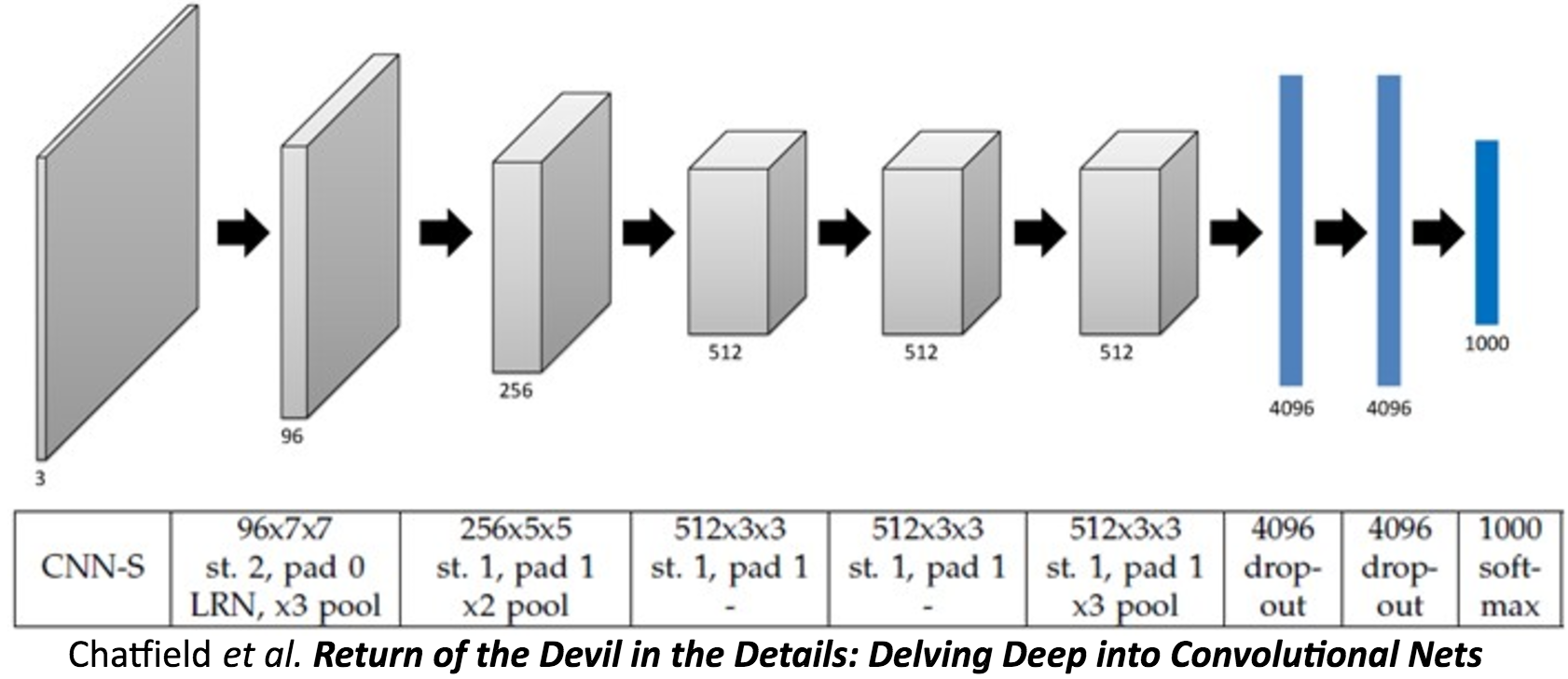
CNN Architecture

</br> </br>

DCGAN Architecture

DCGAN은 결국, 기존 GAN에 존재했던 fully-connected 구조의 대부분을 CNN구조로 대체한것.

![[Architecture guidelines.png]]

• Discriminator에서는 모든 pooling layers를 strided convolutions로 바꾸고, Generator에서는 pooling layers를 fractional-strided convolution으로 바꾼다.

• Generator와 Discriminator에 batch-normalization을 사용한다. 논문에서는 이를 통해deep generators의 초기 실패를 막는다고 하였다. 그러나 모든 layer에 다 적용하면 sample oscillation과 model instability의 문제가 발생하여 Generator output layer와 Discriminator input layer에는 적용하지 않았다고 한다.

• Fully-connected hidden layers를 삭제한다.

• Generator에서 모든 활성화 함수는 ReLU를 쓰되, 마지막 출력단에서만 Tanh를 사용한다.

• Discriminator에서는 모든 활성화 함수를 LeakyReLU를 사용한다.

</br> </br> </br>

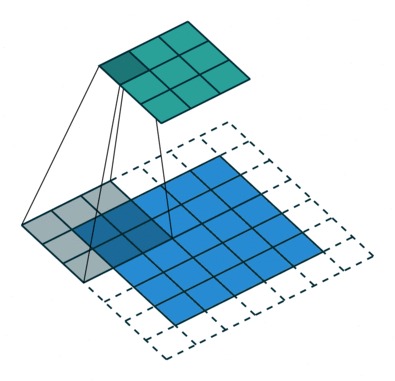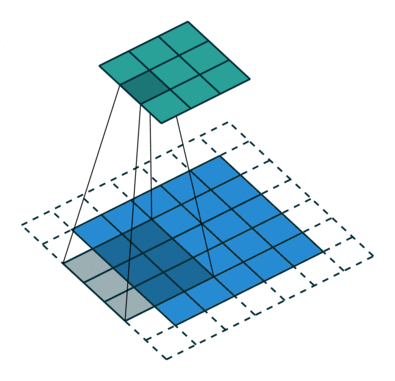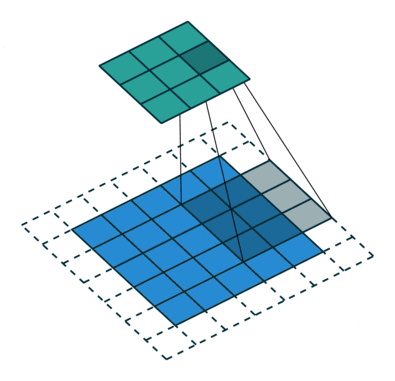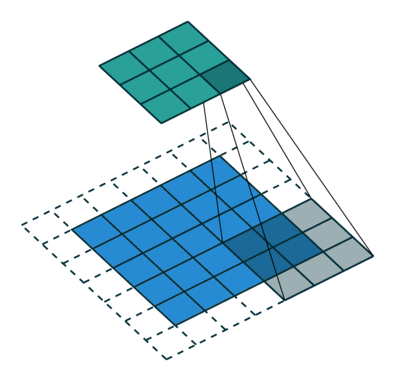
Strided Convolution이란?

</br> </br>

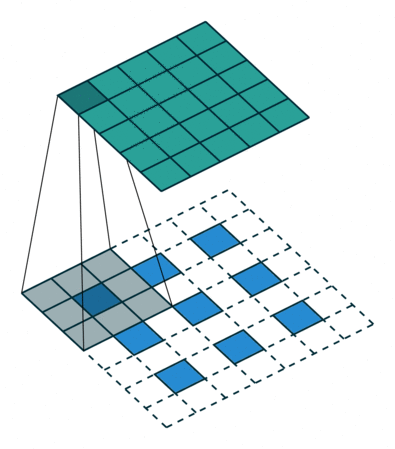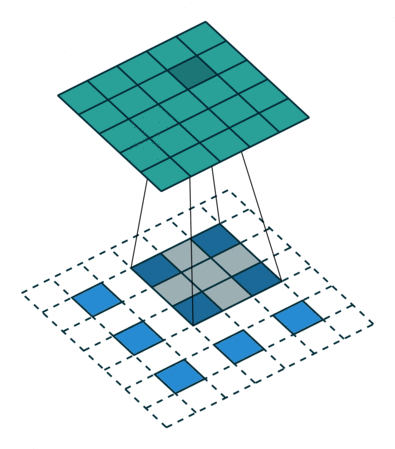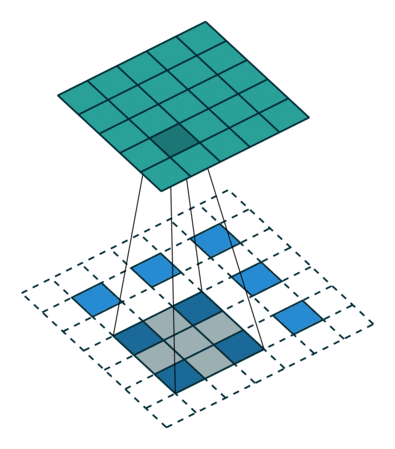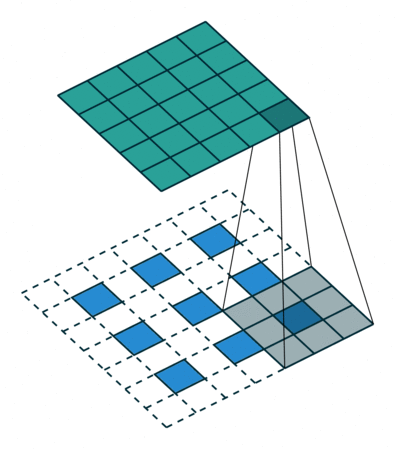
Fractionally-Strided Convolution이란?

둘의 차이는

기존 convolutions는 필터를 거치며 크기가 작아진 반면에 fractionally-strided convolution은 input에 padding을 하고 convolution을 수행하며 오히려 필터가 더 커지는 특징이 차이점 이다.

쉽게 transposed convolution이라고 불린다 논문에서는 Deconvolution이라고 불리는데 이는 잘못된 단어라고 한다.

</br> </br>

Batch-normalization이란?

Batch Normalization은 최근 거의 모든 인경신경망에 쓰이고 있는 기법으로 기본적으로 Gradient Vanishing / Gradient Exploding이 일어나지 않도록 하는 아이디어 중의 하나이며, 지금까지는 이 문제를 Activation함수의 변화(ReLU 등), Careful Initialization, small learning rate 등으로 해결했지만, 이 논문에서는 이러한 간접적인 방법보다 training하는 과정 자체를 전체적으로 안정화하여 학습 속도를 가속시킬 수 있는 근본적인 방법을 제안하였다.

</br> </br>

Gradient Vanishing / Exploding 문제

신경망에서 학습시 Gradient 기반의 방법들은 파라미터 값의 작은 변화가 신경망 출력에 얼마나 영향을 미칠 것인가를 기반으로 파라미터 값을 학습시키게 된다.

만약 파라미터 값의 변화가 신경망 결과의 매우 작은 변화를 미치게 될 경우 파라미터를 효과적으로 학습 시킬 수 없게 된다.

Gradient 라는 것이 결국 미분값 즉 변화량을 의미하는데 이 변화량이 매우 작아지거나(Vanishing) 커진다면(Exploding) 신경망을 효과적으로 학습시키지 못하고, Error rate 가 낮아지지 않고 수렴해버리는 문제가 발생 하게 된다. 

그래서 이러한 문제를 해결하기 위해서 Sigmoid 나 tanh 등의 활성화 함수들은 매우 비선형적인 방식으로 입력 값을 매우 작은 출력 값의 범위로 squash 해버리는데, 가령 sigmoid는 실수 범위의 수를 [0, 1]로 맵핑해버린다.

이렇게 출력의 범위를 설정할 경우, 매우 넓은 입력 값의 범위가 극도로 작은 범위의 결과 값으로 매핑된다.

이러한 현상은 비선형성 레이어들이 여러개 있을 때 더욱 더 효과를 발휘하여(?) 학습이 악화된다. 

첫 레이어의 입력 값에 대해 매우 큰 변화량이 있더라도 결과 값의 변화량은 극소가 되어버리는 것이다. 

그래서 이러한 문제점을 해결하기 위해 활성화 함수로 자주 쓰이는 것이 ReLU(Rectified Linear Unit) 이다. 또한 아래와 같은 방법들도 존재한다. 

• Change activation function : 활성화 함수 중 Sigmoid 에서 이 문제가 발생하기 때문에 ReLU 를 사용
• Careful initialization : 가중치 초기화를 잘 하는 것을 의미
• Small learning rate : Gradient Exploding 문제를 해결하기 위해 learning rate 값을 작게 설정함

</br> </br>

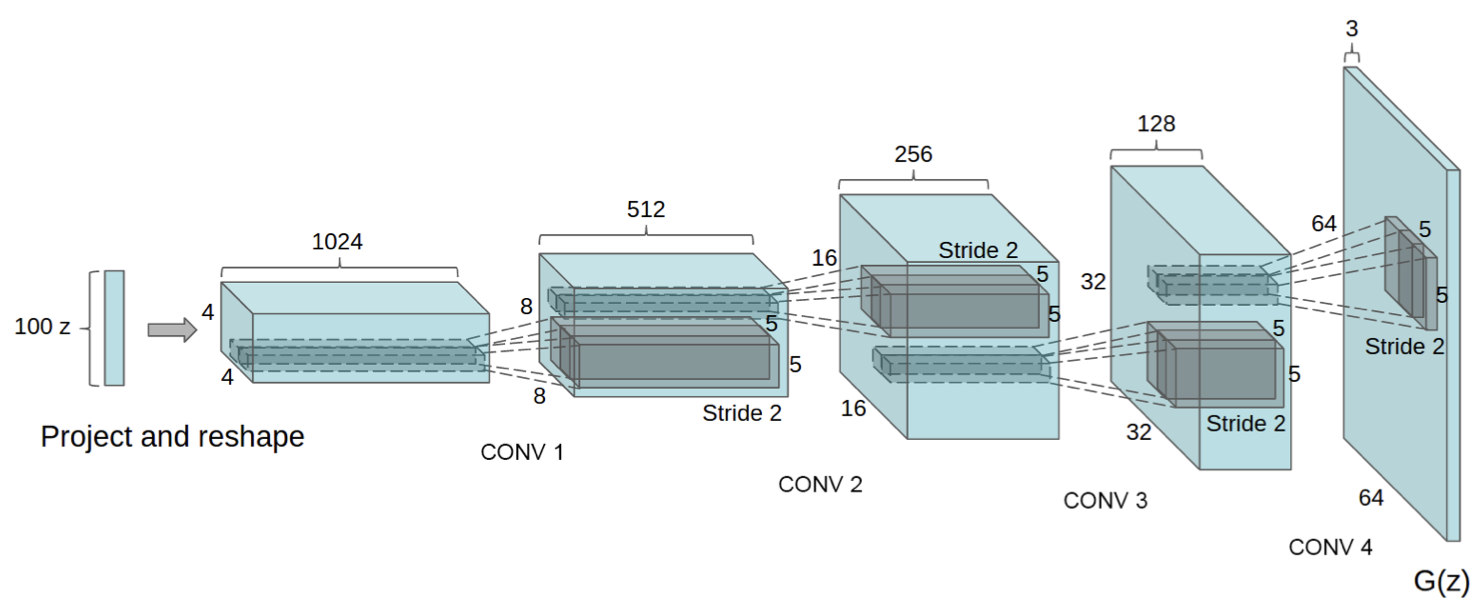
Generator Model

100 dimensional uniform distribution(Z) 이 들어오면 이들이 4개의 fractionally-strided convolution layer를 거치며 크기를 키워서 더 높은 차원의 64 x 64 pixel 이미지가 된다.

</br> </br>

Visualization

Generated bedrooms

Walking in the latent space

앞서 DCGAN의 목표들 중 하나인 walking in the latent space를 직접 구현한 그림.

생성된 2개의 이미지에 사용된 noise인 $z$ 를 선형 보간하며 그 보간된 $z$ 로 이미지를 생성시켜본 결과 한 이미지에서 다른 이미지로 서서히 변해가는 결과를 얻었다. 이미지를 보면 창문 없는 방이 거대한 창문이 있는 방으로 변해가거나, TV가 창문으로 변해가는 과정을 볼 수 있다.

Visualize filters (no longer black-box) 네트워크 내부의 각 필터는 이해할 수 없는 형식이 아닌 특정 object나 특징을 추출하였음을 알 수 있다.

Applying arithmetic in the input space 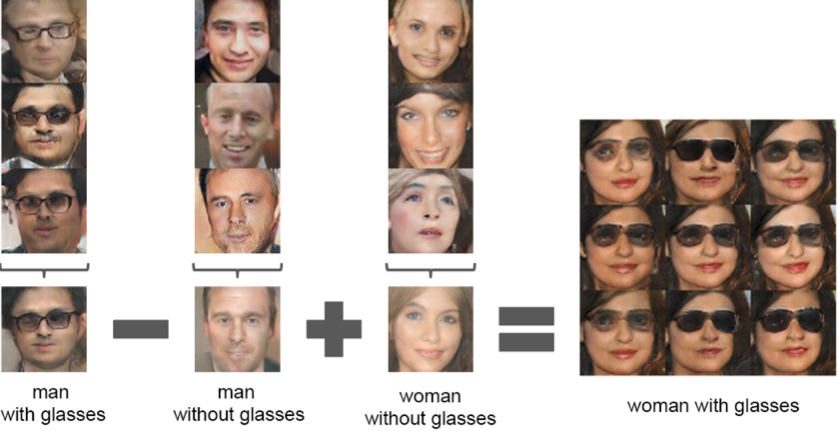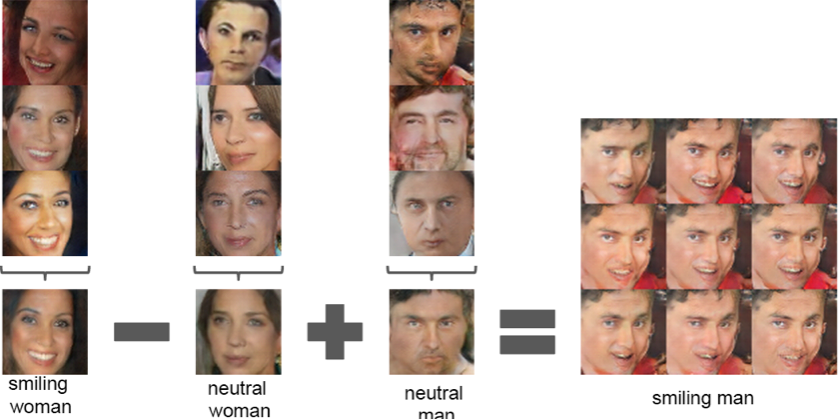벡터 산술 연산을 통해 vec(웃는 여자) - vec(무표정 여자) + vec(무표정 남자) = vec(웃는남자) 같은 결과를 얻을 수 있다.

</br> </br> </br> </br>

DCGAN 구현

Import

from _future_ import print_function

import random
import torch
import torch.nn as nn
import torch.nn,parallel
import torch.backends.cudnn as cudnn
import torch.optim as optim
import torch.utils.data
import torchvision.datasets as dset
import torchvision.transforms as transforms
import torchvision.utils as vutils 
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from IPython.display import HTML

manualSeed = 999
random.seed(manualSeed)
torch.manual_seed(manualSeed)

</br>

Inputs

• dataroot - 데이터셋 폴더의 root경로
• workers - DataLoader를 사용해 데이터를 로드하는데 사용하는 쓰레드 수
• batch_size - 훈련에 사용되는 배치 크기. DCGAN 논문에서는 배치 크기를 128로 사용
• image_size - 훈련에 사용되는 이미지 공간 크기. 이 구현은 기본적으로 $64 \times 64$로 설정 다른 크기를 원하는 경우 D 및 G의 구조를 변경해야 함
• nc - 입력 이미지의 색상 채널 수. color 이미지의 경우 3
• nz - latent vector 길이
• ngf - Generator를 통해 전달되는 feature map의 깊이와 관련
• ndf - Discriminator를 통해 전달되는 feature map의 깊이 설정
• num_epochs - 실행할 훈련 epoch 수. 더 긴 훈련은 보다 나은 결과를 얻을 수 있지만, 오랜 시간 소요
• lr - learning rate. DCGAN논문에서는 0.0002로 설정
• beta1 - Adam 옵티마이저의 beta1 하이퍼파라미터. 논문에서는 0.5로 설정
• ngpu - 사용 가능한 GPU 수. 이 값이 0이면 코드가 CPU모드에서 실행됨. 이 숫자가 0보다 크면 해당 수의 GPU에서 실행

# 데이터셋 폴더의 root경로
dataroot = 'data/celeba'

# DataLoader를 사용해 데이터를 로드하는데 사용하는 쓰레드 수
workers = 8

# 훈련에 사용되는 배치 크기. DCGAN 논문에서는 배치 크기를 128로 사용
batch_size = 128

# 훈련에 사용되는 이미지 공간 크기. 이 구현은 기본적으로 $64 \times 64$로 설정 다른 크기를 원하는 경우 D 및 G의 구조를 변경해야 함
image_size = 64

# 입력 이미지의 색상 채널 수. color 이미지의 경우 3
nc = 3

# latent vector 길이
nz = 100

# Generator를 통해 전달되는 feature map의 깊이와 관련
ngf = 64

# Discriminator를 통해 전달되는 feature map의 깊이 설정
ndf = 64

# 실행할 훈련 epoch 수. 더 긴 훈련은 보다 나은 결과를 얻을 수 있지만, 오랜 시간 소요
num_epochs = 10

# learning rate. DCGAN논문에서는 0.0002로 설정
lr = 0.0002

# Adam 옵티마이저의 beta1 하이퍼파라미터. 논문에서는 0.5로 설정
beta1 = 0.5

# 사용 가능한 GPU 수. 이 값이 0이면 코드가 CPU모드에서 실행됨. 이 숫자가 0보다 크면 해당 수의 GPU에서 실행
ngpu = 1

</br>

Data

# !pip install -U --no-cache-dir gdown --pre
# !gdown --id 1O8LE-FpN79Diu6aCvppH5HwlcR5I--PX
# !mkdir data
# !unzip img_align_celeba.zip -d data/

</br>

Data Load

transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))가 이미지 데이터의 범위를 [-1, 1]로 변경하는 이유는, 이 변환 과정이 각 채널의 픽셀 값에 대해 정규화를 수행하기 때문.

정규화는 다음 공식에 따라 수행 $\text{normalized_pixel} = \frac{\text{pixel} - \text{mean}}{\text{std}}$

여기서,

• pixel은 원본 픽셀 값
• mean은 정규화할 때 사용되는 평균 값
• std는 정규화할 때 사용되는 표준편차 값

transforms.ToTensor()를 통해 이미지는 [0, 1] 범위의 픽셀 값을 가진 텐서로 변환. 이때 (0.5, 0.5, 0.5)를 평균으로 하고, (0.5, 0.5, 0.5)를 표준편차로 사용하여 정규화하면, 결과적으로 픽셀 값의 범위가 [-1, 1]로 조정. 이는 각 채널에서 0.5를 빼고 (평균을 0으로 만들고), 그 결과를 0.5로 나누어 (표준편차를 1로 만들어) 정규화하기 때문

예를 들어, [0, 1] 범위의 픽셀 값에 대해 정규화 과정을 적용

• 픽셀 값이 0.0인 경우: ((0.0 - 0.5) / 0.5 = -1.0)
• 픽셀 값이 1.0인 경우: ((1.0 - 0.5) / 0.5 = 1.0)

따라서, 이 정규화 과정을 통해 픽셀 값의 범위가 [-1, 1]로 조정.

# dset.ImageFolder는 PyTorch의 torchvision.datasets 모듈에 있는 클래스로, 지정된 폴더 구조에서 이미지 데이터를 자동으로 불러온다.
# 이 클래스를 사용하면 이미지와 해당 이미지의 라벨(폴더 이름을 기준으로 자동 할당)을 함께 로드할 수 있다.

# dset.ImageFolder는 각 이미지 파일을 불러올 때 해당 파일이 위치한 폴더 이름을 기반으로 라벨을 자동으로 생성한다. 예를들어 데이터셋 폴더 구조가 
# 'root/dog/xxx.png', 'root/cat/yyy.png'와 같이 구성되어 있다면 dog폴더에 있는 이미지들에는 dog에 해당하는 라벨이 cat 폴더에 있는 
# 이미지 들에는 cat에 해당하는 라벨이 자동으로 할당된다. 이 라벨은 일반적으로 정수 인덱스로 변환되어 관리된다.

# DataLoader를 통해 데이터셋을 배치 단위로 불러올 때, 반환되는 각 배치는 두 부분으로 구성된다. 
# data[0]: 이미지 데이터 텐서. 여기선 전처리 과정을 거친 이미지들이 배치 단위로 포함 
# data[1]: 라벨 데이터 텐서. 이는 dset.ImageFolder에 의해 자동으로 할당된 라벨들이며, 위에서 설명한 대로 폴더 구조를 기반으로 한다.

# 이미지 데이터셋을 로딩하기 위해 ImageFolder 클래스를 사용
dataset = dset.ImageFolder(root = dataroot,
						   # transform은 데이터에 적용할 전처리 목록을 정의
						   transform = transforms.Compose([
								transforms.Resize(image_size),
								transforms.CenterCrop(image_size),
								transforms.ToTensor(),
								# transforms.Normalize(mean, std)
									           #각 채널(RGB)의 평균(mean) # 각 채널의 표준편차(standard deviation)
								transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)),
						   ]))

dataloader = torch.utils.data.DataLoader(dataset, batch_size = batch_size,
										shuffle = True, num_workers = workers)

device = torch.device("cuda:0" if (torch.cuda.is_available() and ngpu > 0) else "cpu")

# 데이터 로더에서 첫 번째 배치를 가져옴. 
# dataloader는 데이터셋에서 미니배치를 순차적으로 로드 
# iter(dataloader)는 dataloader의 iterator를 생성하고, next() 함수는 iterator에서 다음 아이템(여기서는 첫번째 배치)을 가져옴
real_batch = next(iter(dataloader))
plg.figure(figsize = (8, 8))
plt.axis("off")
plt.title("Training Images")


# 실제 이미지 배치를 시각화
# vutils.make_grid() 함수는 여러 이미지를 그리드 형태로 배열하여 하나의 이미지로 만듦
# real_batch[0] 은 데이터 로더로부터 가져온 첫 번째 배치의 이미지 텐서
# [:64] 첫 64개의 이미지만 사용
# padding=2 는 이미지 간의 패딩을 2픽셀로 설정 
# normalize=True 는 이미지 픽셀 값을 [0, 1]범위로 정규화
# np.transpose(..., (1, 2, 0)) 는 텐서의 차원을 변경. PyTorch는 이미지를 (C, H, W) 형식으로 저장하지만, 
# matplotlib은 (H, W, C) 형식을 기대하므로 채널 차원을 맨 뒤로 이동
# 즉 첫번째 배치를 가져와서 거기 있는 64개의 이미지를 그리드로 그리는 코드
plt.imshow(np.transpose(vutils.make_grid(real_batch[0].to(device)[:64], 
										 padding = 2, normalize=True).cpu(),(1, 2, 0))

</br>

Weight Initialization (가중치 초기화)

DCGAN논문에서 저자들은 모든 모델 가중치가 평균 = 0, 표준편차 = 0.02 인 정규 분포에서 무작위로 초기화되어야 한다고 명시 weights_init 함수는 초기화된 모델을 입력으로 받고 모든 Conv2d, Conv2dTranspose 및 BatchNormalization Layer를 이 기준을 충족시키도록 다시 초기화 한다. 이 함수는 모델이 초기화된 직후에 적용

# 가중치 초기화 함수
# 생성자(netG)와 판별자(netD)에 적용
def weights_init(m):
	# 모듈의 클래스 이름 반환
	classname = m.__class__.__name__
	if classname.find('Conv') != -1:
		# nn.init.normal_ 함수는 주어진 텐서를 in-place로 정규 분포를 사용해 초기화
		# 여기서 m.weight.data는 해당 층의 가중치 텐서를 의미하며, 평균 0.0, 표준펀차 0.02의 분포를 사용
		nn.init.normal_(m.weight.data, 0.0, 0.02)
	elif classname.find('BatchNorm') != -1:
		nn.init.normal_(m.weight.data, 1.0, 0.02)
		nn.init.constant_(m.bias.data, 0)

</br>

Generator

Generator $G$ 는 잠재 공간 벡터 ($z$) 를 데이터 공간으로 매핑하는 것이 목표. $z$ 를 데이터 공간으로 변환하면 최종적으로 훈련 이미지와 동일한 크기의 RGB 이미지를 만드는것 (즉 $3\times64\times64$) 실제로는 일련의 스트라이드된 2차원 Conv2dTranspose layer와 각각의 2차원 BatchNormalization layer와 ReLU Activation 함수와 함께 이를 수행, Generator의 출력은 tanh 함수를 통해 다시 입력 데이터 범위인 $[-1, 1]$ 로 변환. DCGAN 논문에서 BatchNormalization 함수의 존재를 언급하는 것이 중요하다. 이러한 레이어들은 훈련 중에 경사하강법(gradient-descent)의 흐름을 돕는 중요한 역할을 수행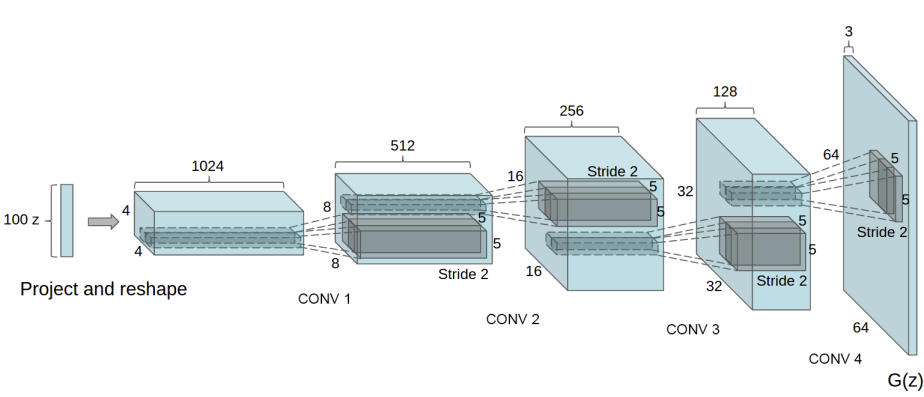

입력 섹션에서 설정한 입력(nz, ngf, nc)이 코드에서 Generator 아키텍쳐에 영향을 미치는 방식에 주목하면 nz는 z의 입력 벡터의 길이이고, ngf는 생성기를 통해 전달되는 feature map의 크기와 관련이 있으며, nc는 출력 이미지의 채널 수(RGB 이미지의 경우 3으로 설정)

</br>

"""
# 입력 이미지의 색상 채널 수. color 이미지의 경우 3
nc = 3

# latent vector 길이
nz = 100

# Generator를 통해 전달되는 feature map의 깊이와 관련
ngf = 64

# Discriminator를 통해 전달되는 feature map의 깊이 설정
ndf = 64
"""
class Generator(nn.Module):
	def __init__(self, ngpu):
		super(Generator, self).__init__()
		self.ngpu = gpu
		self.main = nn.Sequential(
			# nz는 입력 벡터(z)의 차원, ngf는 생성자의 피처 맵 수
			# 이 층은 nz 차원의 입력을 받아 ngf*8 채널의 피처 맵을 출력
			nn.ConvTranspose2d(in_channels = nz, out_channels = ngf * 8,
							   kernel_size = 4, stride = 1,
							   padding = 0, bias = False),
			nn.BatchNorm2d(ngf * 8),
			nn.ReLU(inplace = True),
			# 출력 크기:  (ngf*8) x 4 x 4
			
			nn.ConvTranspose2d(ngf * 8, ngf * 4, 4, 2, 1, bias=False),
			nn.BatchNorm2d(ngf * 4),
			nn.ReLU(True),
			# 출력 크기: (ngf*4) x 8 x 8
			
			nn.ConvTranspose2d(ngf * 4, ngf * 2, 4, 2, 1, bias=False),
			nn.BatchNorm2d(ngf * 2),
			nn.ReLU(True),
			# 출력 크기: (ngf*2) x 16 x 16
			
			nn.ConvTranspose2d(ngf * 2, ngf, 4, 2, 1, bias=False),
			nn.BatchNorm2d(ngf),
			nn.ReLU(True),
			# 출력 크기: (ngf) x 32 x 32
			
			# 마지막 층: 최종 이미지를 생성
			# 출력 채널 수(nc)는 생성할 이미지의 채널 수
			nn.ConvTranspose2d(ngf, nc, 4, 2, 1, bias=False),
			nn.Tanh()
			# 출력 크기는 (nc) x 64 x 64가 됩니다. 
			# 활성화 함수로 Tanh를 사용하여 출력 값을 [-1, 1] 범위로 조정합니다.
			
		)

	def forward(self, input):
		return self.main(input)		

</br>

nn.ConvTranspose2d는 전치 합성곱(transposed convolution) 또는 분수 스트라이드 합성곱(fractionally-strided convolution)을 수행하여 입력 데이터의 공간 차원을 확장 이 과정에서 입력 텐서의 크기를 (nz, 1, 1)에서 시작하여 더 큰 공간 차원으로 변환 가능
nz가 100이라고 할 때, in_channels=nz는 입력 채널의 수를 의미 여기서 주목해야 할 점은 전치 합성곱이 입력의 공간적 차원을 어떻게 확장하는지이다.

전치 합성곱 층의 출력 크기는 다음과 같은 공식에 의해 결정된다. \(\text{H}_{\text{out}} = (\text{H}_{\text{in}} - 1) \times \text{stride} - 2 \times \text{padding} + \text{kernel\_size}\)

여기서,

• $( \text{H}_{\text{out}})$은 출력 높이,
• $( \text{H}_{\text{in}} )$은 입력 높이 (이 경우 1),
• stride는 스트라이드 값 (이 경우 1),
• padding은 패딩 값 (이 경우 0),
• kernel_size는 커널 크기 (이 경우 4)

이 공식을 사용하면 첫 번째 nn.ConvTranspose2d 층의 출력 높이와 너비가 어떻게 결정되는지 계산 가능하다.

\(\text{H}_{\text{out}} = (1 - 1) \times 1 - 2 \times 0 + 4 = 4\) 따라서, 첫 번째 nn.ConvTranspose2d 층의 출력은 (ngf*8, 4, 4)의 차원을 가지게 된다. 여기서 ngf*8은 이 층의 출력 채널 수. ngf는 생성자의 기본 필터 수를 의미하는 하이퍼파라미터이며, 이를 통해 모델의 용량을 조절할 수 있다.

요약하자면, 이 코드는 nz 차원의 잠재 벡터를 입력으로 받아, 내부적으로 공간 차원을 확장하는 전치 합성곱 연산을 수행하여 최종적으로 (ngf*8, 4, 4) 크기의 텐서를 출력한다. 이 과정은 초기 잠재 벡터에서 시작하여 점차적으로 이미지와 같은 고차원 데이터를 생성하는 과정을 구현한다.

</br> </br>

Why $z$ = 100?

z가 100이여도 1이여도 nn.ConvTranspose2d 층의 출력 크기는 동일하다. 하지만 z의 차원 수, 즉 잠재 벡터(z)의 크기를 1이 아닌 100과 같이 더 크게 설정하는 이유는, 모델이 학습할 수 있는 표현력과 다양성에 있다. 잠재 벡터의 크기가 커질수록, 생성자는 더 다양하고 복잡한 패턴과 특성을 학습하여 생성할 수 있는 가능성이 높아진다.

</br>

1. 표현력(Expressiveness)

• 잠재 공간이 더 크면, 모델이 학습할 수 있는 데이터의 특성이 더 많아진다. 즉, 더 다양한 이미지를 생성할 수 있는 가능성이 커진다. z가 단일 차원이면, 이론적으로는 매우 제한적인 변화만 표현할 수 있다.

</br>

2. 다양성(Diversity)

• 더 큰 차원의 잠재 벡터는 생성된 이미지 간에 더 큰 다양성을 가능하게 한다. 잠재 공간의 각 차원은 생성 과정에서 다른 종류의 변화를 조절할 수 있으므로, 더 많은 차원을 가지면 더 세밀하고 다양한 이미지를 생성할 수 있다.

</br>

3. 학습의 용이성(Learnability)

• 잠재 벡터의 차원이 너무 작으면, 생성자가 학습 데이터의 복잡성을 충분히 모델링하기 어려울 수 있다. 적절한 크기의 잠재 공간은 학습 과정에서 모델이 데이터 분포를 더 잘 학습하게 만들 수 있다.

</br>

4. 실제 적용에서의 고려 사항

• z의 차원을 결정할 때는, 생성하고자 하는 데이터의 복잡성, 모델의 구조, 그리고 학습 과정에서의 계산 비용 등을 고려해야 한다. 너무 큰 차원은 모델의 학습을 어렵게 만들고, 계산 비용을 증가시킬 수 있다.

결론적으로, 잠재 벡터 z의 차원 수는 생성자가 생성할 수 있는 이미지의 품질과 다양성에 중요한 영향을 미친다. 따라서 z의 차원을 1로 설정하는 것과 100으로 설정하는 것 사이에는 생성된 이미지의 품질과 다양성 측면에서 큰 차이가 있을 수 있다. 적절한 차원 수는 실험을 통해 결정되며, 대상 데이터와 특정 응용 프로그램의 요구 사항에 따라 달라질 수 있다.

</br> </br>

Generator 가중치 초기화

이제 Generator를 인스턴스화 하고 weights_init 함수를 적용할 수 있다.

netG = Generator(ngpu).to(device)

if (device.type == 'cuda') and (ngpu > 1):
	netG = nn.DataParallel(netG, list(range(ngpu)))

# Generator 가중치 초기화
netG.apply(weights_init)

print(netG)

"""
Generator(
  (main): Sequential(
    (0): ConvTranspose2d(100, 512, kernel_size=(4, 4), stride=(1, 1), bias=False)
    (1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (2): ReLU(inplace=True)
    (3): ConvTranspose2d(512, 256, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
    (4): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (5): ReLU(inplace=True)
    (6): ConvTranspose2d(256, 128, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
    (7): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (8): ReLU(inplace=True)
    (9): ConvTranspose2d(128, 64, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
    (10): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (11): ReLU(inplace=True)
    (12): ConvTranspose2d(64, 3, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
    (13): Tanh()
  )
)
"""

</br> </br>

멀티 GPU 사용

멀티 GPU 설정이 작동하는 방식을 이해하려면, PyTorch의 nn.DataParallel 모듈의 역할을 살펴볼 필요가 있다. Generator 클래스에 ngpu 인자를 넣는 것 자체로는 멀티 GPU에서 동작하도록 만들지 않는다. 실제로 멀티 GPU 설정을 가능하게 하는 것은 nn.DataParallel을 사용하는 부분이다.

nn.DataParallel의 역할

• 모델 복제: nn.DataParallel은 모델을 자동으로 여러 GPU에 복제한다. 즉, 각 GPU에 모델의 복사본이 생성되어 동시에 작동할 수 있게 된다.
• 데이터 분할: 입력 데이터 배치가 nn.DataParallel에 의해 자동으로 여러 부분으로 나뉘며, 각각의 GPU에 분배된다. 이렇게 하여 각 GPU는 데이터의 한 부분을 처리하게 된다.
• 병렬 처리: 각 GPU에서는 모델의 복사본을 사용하여 할당받은 데이터 부분을 독립적으로 처리한다. 이 과정은 병렬적으로 수행된다.
• 결과 수집: 각 GPU에서 처리된 결과는 자동으로 한곳에 모아진다. 그리고 필요한 경우 결과들이 합쳐져 최종 출력이 생성된다.

</br> </br>

코드 설명

netG = Generator(ngpu).to(device)

• 여기서 Generator 인스턴스는 단일 GPU 또는 CPU로 이동된다. ngpu는 생성자에 전달되지만, Generator 내부에서는 별도로 멀티 GPU 설정에 사용되지 않는다.

if (device.type == 'cuda') and (ngpu > 1):
    netG = nn.DataParallel(netG, list(range(ngpu)))

• 이 조건문은 CUDA 환경이고 사용 가능한 GPU의 수(ngpu)가 1보다 클 때만 실행된다. nn.DataParallel을 사용하여 netG 모델을 감싸는 것으로 멀티 GPU 설정이 활성화된다.
• list(range(ngpu))는 사용할 GPU의 인덱스 리스트를 생성. 예를 들어, ngpu가 2라면 [0, 1]이 되어 첫 번째와 두 번째 GPU를 사용하게 된다.

결론적으로, Generator 클래스에 ngpu를 전달하는 것은 모델이 몇 개의 GPU를 기대하는지 알려주는 용도로만 사용된다. 실제 멀티 GPU 활성화와 데이터의 병렬 처리는 nn.DataParallel에 의해 이루어진다. nn.DataParallel은 모델을 여러 GPU에 분산시켜 병렬 처리를 가능하게 하는 핵심 메커니즘이다.

</br> </br>

Discriminator

$D$ 는 이미지를 입력으로 받고 해당 입력 이미지가 실제(가짜가 아닌)임을 나타내는 스칼라 확률을 출력하는 이진 분류 네트워크이다. 여기서 $D$는 $3\times64\times64$ 입력 이미지를 받아 Conv2d, BatchNorm2d 및 LeakyReLU 레이어를 통해 처리하고 Sigmoid 활성화 함수를 통해 최종 확률을 출력한다. 이 아키텍쳐는 문제에 따라 더 많은 레이어로 확장될 수 있지만 strided convolution, BatchNorm 및 LeakyReLU의 사용에는 의미가 있다. DCGAN 논문에서는 네트워크가 자체 Pooling 함수를 학습할 수 있도록 strided convolution을 사용하는 것이 좋은 실천 방법이라고 언급한다. 또한 배치 정규화 및 LeakyReLU 함수는 $G$와 $D$의 학습 과정에 대한 건전한 기울기 흐름을 촉진하는데 중요하다.

\(\text{output\_size} = \left\lfloor \frac{\text{input\_size} + 2 \times \text{padding} - \text{kernel\_size}}{\text{stride}} \right\rfloor + 1\)

class Discriminator(nn.Module):
	def __init__(self, ngpu):
		super(Discriminator, self).__init__()
		self.ngpu = ngpu
		self.main = nn.Sequential(
			# input is (nc) x 64 x 64
			nn.Conv2d(in_channels = nc, out_channels = ndf,
					  kernel_size = 4, strides = 2,
					  padding = 1, bias = False),
			nn.LeakyReLU(0.2, inplace = True),
			# state size. (ndf) x 32 x 32
			nn.Conv2d(ndf, ndf * 2, 4, 2, 1, bias=False),
			nn.BatchNorm2d(ndf * 2),
			nn.LeakyReLU(0.2, inplace=True),
			# state size. (ndf*2) x 16 x 16
			nn.Conv2d(ndf * 2, ndf * 4, 4, 2, 1, bias=False),
			nn.BatchNorm2d(ndf * 4),
			nn.LeakyReLU(0.2, inplace=True),
			# state size. (ndf*4) x 8 x 8
			nn.Conv2d(ndf * 4, ndf * 8, 4, 2, 1, bias=False),
			nn.BatchNorm2d(ndf * 8),
			nn.LeakyReLU(0.2, inplace=True),
			# state size. (ndf*8) x 4 x 4
			nn.Conv2d(ndf * 8, 1, 4, 1, 0, bias=False),
			nn.Sigmoid()
		)
	def forward(self, input):
		return self.main(input)

# Create the Discriminator
netD = Discriminator(ngpu).to(device)

# Handle multi-gpu if desired
if (device.type == 'cuda') and (ngpu > 1):
	netD = nn.DataParallel(netD, list(range(ngpu)))

# Apply the weights_init function to randomly initialize all weights
# to mean=0, stdev=0.2.
netD.apply(weights_init)

# Print the model
print(netD)

"""
Discriminator(
  (main): Sequential(
    (0): Conv2d(3, 64, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
    (1): LeakyReLU(negative_slope=0.2, inplace=True)
    (2): Conv2d(64, 128, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
    (3): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (4): LeakyReLU(negative_slope=0.2, inplace=True)
    (5): Conv2d(128, 256, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
    (6): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (7): LeakyReLU(negative_slope=0.2, inplace=True)
    (8): Conv2d(256, 512, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)
    (9): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (10): LeakyReLU(negative_slope=0.2, inplace=True)
    (11): Conv2d(512, 1, kernel_size=(4, 4), stride=(1, 1), bias=False)
    (12): Sigmoid()
  )
)
"""

</br> </br>

Loss Functions and Optimizers

$D$ 와 $G$를 설정했으므로, 손실 함수와 옵티마이저를 통해 학습하는 방법을 지정할 수 있다. PyTorch에 정의된 Binary Cross Entropy Loss(BCELoss)함수를 사용한다.

\(\begin{align}\ell(x, y) = L = \{l_1,\dots,l_N\}^\top, \quad l_n = - \left[ y_n \cdot \log x_n + (1 - y_n) \cdot \log (1 - x_n) \right]\end{align}\) 이 함수는 목적 함수의 로그 구성요소를 모두 계산해 준다. $log(D(x))$ 및 $log(1-D(G(z)))$
$y$ 입력을 사용해 BCE 방정식의 어떤 부분을 사용할지 지정할 수 있다. 이는 뒷 부분의 training loop에서 수행되지만, $y$를 변경함으로써 원하는 구성요소를 계산할 수 있다는 것을 이해해야한다.

다음으로, 실제 레이블을 1로, 가짜 레이블을 0으로 정의한다. 이러한 레이블은 $D$와 $G$의 손실을 계산할 때 사용되며, 이는 원래 GAN논문에서 사용된 규약이다. 마지막으로, $D$와 $G$각각에 대한 두 개의 별도의 옵티마이저를 설정한다. DCGAN 논문에서 명시된대로, 둘 다 학습률이 0.0002이고 Beta1이 0.5인 Adam 옵티마이저이다. 생성기의 학습 진행 상황을 추적하기 위해 가우스 분포에서 추출된 고정의 배치 잠재 벡터를 생성한다. (즉 fixed_noise) 훈련 루프에서 이 fixed_noise를 주기적으로 $G$에 입력하고 반복될 때마다 노이즈에서 이미지가 형성되는것을 확인한다.

# Binary Cross Entropy Loss를 초기화 
# 이는 GAN에서 Discriminator가 실제 이미지와 가짜 이미지를 얼마나 잘 구분하는지를 측정하는데 사용
# 생성자가 생성한 이미지를 진짜로, 실제 이미지를 가짜로 판별하지 않도록 학습하는데 이 손실함수가 사용된다.
criterion = nn.BCELoss()

# 고정된 잠재 벡터(fixed noise)배치를 생성한다. 
# 이 벡터는 학습 과정에서 Generator의 진행 상황을 시각화 하기 위해 사용된다.
# 64 = 고정된 노이즈 벡터의 배치 크기(배치 사이즈와 무관) 
# 학습에 사용되는것이 아닌 학습 과정에서 생성자(G)의 성능을 시각적으로 모니터링하는 데 사용 `64`는 한 번에 생성하고자 하는 이미지의 수를 의미
# nz = 잠재 벡터의 차원
fixed_noise = torch.randn(64, nz, 1, 1, device = device) # (64, 100, 1, 1)

real_label = 1.
fake_label = 0.

# Generator와 Discriminator를 위한 Adam 최적화 알고리즘을 설정
# optim.Adam은 모멘텀 항(betas) 메개변수로 받아 최적화를 진행
# .parameters()는 각각의 G 와 D의 학습 가능한 매개변수
optimizerD = optim.Adam(netD.parameters(), lr = lr, betas=(beta1, 0.999))
optimizerG = optim.Adam(netG.parameters(), lr = lr, betas=(beta1, 0.999))

</br> </br>

Training

GAN을 훈련하는 것은 어느 정도 예술의 영역이며, 잘못된 하이퍼파라미터 설정은 모드 붕괴를 초래해 무엇이 잘못되었는지 설명하기 어렵다. 여기서는 Goodfellow의 논문에서 제시한 Algorithm 1을 밀접하게 따르며 ganhacks의 몇가지 모범 사례를 준수한다. 구체적으로 실제와 가짜 이미지에 대해 서로 다른 미니배치를 생성 하고 또한 G의 목적 함수를 최대화 하기 위해 $logD(G(z))$ 로 조정한다. 훈련은 두가지 주요 부분으로 나뉜다. Part1은 Discriminator를 업데이터 하고 Part2는 Generator를 업데이트 한다.

</br>

Part1 - Discriminator training

Discriminator를 훈련시키는 목표는 주어진 입력을 실제 또는 가짜로 올바르게 분류할 확률을 최대화 하는 것이다. Goodfellow에 따르면 확률적 경사 상승을 통해 구분자를 업데이트 한다. 실제로 $log(D(x)) + log(1-D(G(z)))$를 최대화 할 것이다. ganhacks의 분리된 미니 배치를 제안으로 인해 이를 두 단계로 계산한다. 먼저 훈련 세트에서 실제 샘플 배치를 구성하고 $D$를 통해 전방향으로 전달해 손실 $log(1-D(G(z)))$ 를 계산하고 역전파로 그라디언트를 누적한다.

</br>

Part2 - Generator training

원 논문에서는 더 나은 가짜 이미지를 생성하기 위해 $log(1-D(G(z)))$ 를 최소화하여 Generator를 훈련시킨다. 하지만 특히 학습 초기에는 충분한 그라디언트를 제공하지 않으므로 이를 수정하기 위해 대신 $log(D(G(z)))$를 최대화 한다. 이는 Part1에서 생성된 Generator 출력을 Discriminator로 분류하고, 실제 레이블을 GT로 사용하여 G의 손실을 계산하고 역전파로 G의 그라디언트를 계산한 후에, 옵티마이저 단계로 G의 매개변수를 업데이트 한다. 손실 함수에 실제 레이블을 GT레이블로 사용하는 것이 직관적이지 않을 수 있지만 이렇게 하면 BCELoss의 $log(x)$ 부분을 사용할 수 있다 ( $log(1-x)$ 부분 대신 )

마지막으로 각 epoch 마다 고정된 잠재 벡터 배치를 Generator에 넣어 Generator의 훈련 진행 상황을 시각적으로 추적한다.

• Loss_D : 모든 실제 및 가짜 배치의 손실로 계산된 Discriminator Loss ($log(D(x)) + log(1-D(G(z)))$ )
• Loss_G : 생성자 손실로 계산된 $log(D(G(z)))$
• $D(x)$ : 실제 배치에 대한 구분자의 평균을 출력. 이는 처음에는 1에 가까워야 하며 이론적으로 G가 더 좋아질 때 0.5로 수렴해야 한다.
• $D(G(z))$ : 모든 가짜 배치에 대한 구분자의 평균. 이는 처음에는 0에 가깝게 시작하고 G가 더 좋아질 때 0.5로 수렴해야 한다.

</br>

# PIL 라이브러리에서 트리머이션된(일부만 로드된)이미지를 로드할 수 있도록 설정. 
# 이는 이미지 파일이 손상되었거나 제대로 로드되지 않았을 때 오류를 방지하는데 도움
from PIL import ImageFile
imageFile.LOAD_TRUNCATED_IMAGES = True

# 학습 과정을 추적하기 위한 리스트 초기화
# img_list 는 생성자의 출력 예시를 저장
# G_losses와 D_losses는 각각 생성자와 판별자의 손실을 저장 
# iters 는 반복 횟수를 추적 
img_list = []
G_losses = []
D_losses = []
iters = 0

print("Starting Training Loop...")

# 지정된 에폭 수(num_epochs)만큼 반복하며, 각 에폭에 대해 데이터 로더에서 배치 데이터를 순회
for epoch in range(num_epochs):
	for i, data in enumerate(dataloader, 0):

		# Discriminator 업데이트. 판별자의 목표는 실제이미지를 진짜로, 생성된 가짜 이미지를 가짜로 정확하게 분류하는 것 
		# 즉 log(D(x)) + log(1 - D(G(z)))를 최대화 하는 것(최대가 0임)

		# Discriminator의 그래디언트 초기화. 이는 역전파 단계에서 그래디언트를 새로 계산하기 전에 필요한 단계
		netD.zero_gard()

		# 실제 데이터 배치를 형식에 맞게 조정하고, 실제 이미지에 대한 레이블을 생성
		real_cpu = data[0].to(device) # data[0] : [128, 3, 28, 28](튜플 형태)
		b_size = real_cpu.size(dim = 0)
		label = torch.full((b_size, ), real_label, dtype = torch.float, device = device)

		# 실제 이미지 배치를 Discriminator에 통과시키고, 실제 이미지에 대한 손실을 계산한 후, 그래디언트 역전파
		output = netD(real_cpu).view(-1) # 텐서를 1차원으로 평탄화(flatten)
		errD_real = criterion(output, label)
		errD_real.backward()
		D_x = output.mean().item()

		# 가짜 이미지 배치를 생성하기 위한 잠재 벡터 생성 
		noise = torch.randn(b_size, nz, 1, 1, device = device)
		
		# 생성자를 사용해 가짜 이미지 배치를 생성하고, 가짜 이미지에 대한 레이블을 설정
		fake = netG(noise)
		label.full_(fake_label)

		# 생성된 가짜 이미지 배치를 판별자에 통과시키고, 가짜 이미지에 대한 손실을 계산한 후, 그래디언트 역전파
		# .detach() 메서드의 주요 목적은 해당 텐서에 대한 연산이 이후의 그래디언트 계산에서 제외되도록 하는 것.
		# fake.detach()는 fake 텐서로 부터 그래디언트가 역전파 되는 것을 방지.
		# 이는 생성자(netG)에 대한 가중치 업데이트를 방지하고, Discriminator만을 학습시키기 위한 목적.
		output = netD(fake.detach()).view(-1)
		errD_fake = criterion(output, label)
		errD_fake.backward()
		D_G_z1 = output.mean().item()

		# 실제 이미지와 가짜 이미지에 대한 손실을 합산해 Discriminator의 총 손실을 계산하고, 
		# 이를 기반으로 Discriminator의 매개변수 업데이트
		errD = errD_real + errD_fake
		optimizerD.setp()

		
		# Generator 업데이트. Generator의 목표는 Discriminator를 속여 가짜 이미지를 진짜로 분류하도록 만드는 것
		# 즉 log(D(G(z)))를 최대화 하는 것. (최대가 0임)

		# Generator의 그래디언트를 초기화하고, 생성된 가짜 이미지를 진짜로 분류하도록 하는 레이블 설정.
		# Generator는 Discriminator를 속이려고 하므로, 생성된 이미지에 대해 진짜 레이블을 사용
		netG.zero_gard()
		label.fill_(real_label)

		# Discriminator를 최신 상태로 업데이트한 후, 같은 가짜 이미지 배치를 다시 Discriminator에 통과시키고, 이에 대한 
		# Generator의 손실을 계산. 그 후, 생성자의 그래디언트를 역전파하고 매개변수 업데이트 
		output = netD(fake).view(-1)
		errG = criterion(output, label)
		errG.backward()
		D_G_z2 = output.mean().item()
		optimizerG.step()

		# 훈련 상태 출력 
		if i % 50 == 0:
			# 현재 에폭, 총 에폭 수, 데이터 로더 내의 현재 배치 인덱스, 총 배치 수, 판별자와 생성자의 손실, 
			# 진짜 이미지에 대한 판별자의 평균 출력 값(D_x), 가짜 이미지에 대한 판별자의 출력값(D_G_z1, D_G_z2)을 출력
			print('[%d/%d][%d/%d]\tLoss_D: %.4f\tLoss_G: %.4f\tD(x): %.4f\tD(G(z)): %.4f / %.4f'
					% (epoch, num_epochs, i, len(dataloader), errD.item(), errG.item(), D_x, D_G_z1, D_G_z2))

		# 손실값을 저장하여 나중에 그래프로 그릴 수 있도록 함
		G_losses.append(errG.item()) # 생성자 손실 저장
		D_losses.append(errD.item()) # 판별자 손실 저장

		# 생성자의 성능을 평가하기 위해 fixed_noise를 사용해 생성된 이미지를 저장
		if (iters % 500 == 0) or ((epoch == num_epochs-1) and (i == len(dataloader) - 1)):
			with torch.no_grad(): # 그래디언트 계산을 비활성화 하여 메모리 사용량을 줄이고 계산속도를 높임
				fake = netG(fixed_noise).detach().cpu() # fixed_noise로 부터 생성된 가짜 이미지 생성
			# 생성된 이미지를 그리드 형태로 반환하여 리스트에 저장
			img_list.append(vutils.make_grid(fake, padding = 2, normalize = True)) 
		iters += 1

GAN(생성적 적대 신경망)에서 생성자(G)와 판별자(D)는 서로 경쟁하며 학습한다. 이 과정에서 D의 그래디언트를 업데이트할 때 G에서 생성된 값(가짜 이미지)을 사용하는 경우, detach()를 사용하는 것이 일반적인 규칙이다.

이 규칙의 목적과 조건은 다음과 같다:

목적:

• 판별자(D) 학습: D의 그래디언트를 업데이트할 때는 G에서 생성된 가짜 이미지에 대한 D의 판단(가짜 이미지를 얼마나 잘 구분하는지)을 학습시키려고 한다. 이때, G의 매개변수는 고정되어야 하며, G에 대한 그래디언트 계산은 수행하지 않는다.
• 생성자(G)와의 독립적 학습: D를 학습하는 동안 G는 학습되지 않아야 한다. 즉, G에서 생성된 가짜 이미지를 D에 통과시킬 때, G에 대한 그래디언트는 역전파되지 않아야 힌다. 이렇게 하여 D의 학습이 G의 매개변수에 영향을 주지 않도록 한다.

</br>

조건 및 공식:

• 판별자(D)의 손실 함수 업데이트:
  • 실제 이미지에 대한 D의 손실: $L_D^{real} = -\log(D(x))$, 여기서 $x$는 실제 이미지
  • 가짜 이미지에 대한 D의 손실: $L_D^{fake} = -\log(1 - D(G(z).detach()))$, 여기서 $z$는 잠재 벡터, $G(z)$는 G가 생성한 가짜 이미지.detach()는 $G(z)$의 그래디언트가 D의 업데이트에 사용되지 않도록 한다.
• 판별자(D)의 그래디언트 업데이트:
  • D의 총 손실: $L_D = L_D^{real} + L_D^{fake}$
  • 이 손실을 사용하여 D의 매개변수에 대한 그래디언트를 계산하고 업데이트한다.

</br>

요약:

G에서 생성된 모든 값에 detach()를 붙이는 것은 D를 학습할 때 G의 매개변수가 업데이트되지 않도록 하기 위함. 이는 D의 학습 과정에서만 D의 매개변수가 업데이트되도록 보장한다. 반대로 G를 학습할 때는 D의 출력값에 detach()를 사용하지 않으며, G의 손실 함수를 통해 G의 매개변수를 업데이트한다.

</br> </br> </br>

Results

훈련 중 D와 G의 손실이 어떻게 변화했는지를 살펴보고, 각 epoch마다 fixed_noise 배치에 대한 G의 출력을 시각화, 마지막으로 실제 데이터 배치와 G에서 생성된 가짜 데이터 배치를 비교

</br>

훈련 반복에 따른 손실

plt.figure(figsize = (10 ,5))
plt.title('Generator and Discriminator Loss During Training')
plt.plot(G_losses, label = "G")
plt.plot(D_losses, label = "D")
plt.xlabel("iterations")
plt.ylabel("Loss")
plt.legend()
plt.show()

fig = plt.figure(figsize = (8, 8))
plt.axis("off")
# img 리스트 생성: 애니메이션에 포함될 이미지 프레임들을 담은 리스트
ims = [[plt.imshow(np.transpose(i (1, 2, 0)), animated=True)] for i in img_list]
# ArtistAnimation 객체 생성 : img리스트를 사용해 애니메이션 생성
# blit: 빠른 애니메이션 생성을 위해 True로 설정
ani = animation.ArtistAnimation(fig, ims, interval=1000, repeat_delay=1000, blit=True)

# ani 객체를 Javascript HTML형식으로 변환하여 웹 프라우저에 표시
HTML(ani.to_jshtml())

# Grab a batch of real images from the dataloader
real_batch = next(iter(dataloader))

# Plot the real images
plt.figure(figsize=(15,15))
plt.subplot(1,2,1)
plt.axis("off")
plt.title("Real Images")
plt.imshow(np.transpose(vutils.make_grid(real_batch[0].to(device)[:64], padding=5, normalize=True).cpu(),(1,2,0)))

  
# Plot the fake images from the last epoch
plt.subplot(1,2,2)
plt.axis("off")
plt.title("Fake Images")
plt.imshow(np.transpose(img_list[-1],(1,2,0)))
plt.show()