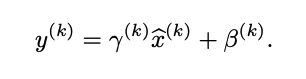Batch Normalization 논문 리뷰
| 태그 | #Normalization |
|---|---|
| 한줄요약 | Batch Normalization |
| Journal/Conference | #ICML |
| Link | Batch Normalization |
| Year(출판년도) | 2015 |
| 저자 | Sergey Ioffe, Christian Szegedy |
| 원문 링크 | Batch Normalization |
쉬운 설명
핵심 요약
- Batch Normalization은 2015년에 소개된, 딥러닝 모델 훈련을 획기적으로 개선한 기법이다.
- 높은 학습 속도를 사용해도 안정적이고, 별도의 복잡한 기법 없이도 모델의 일반화 성능을 높여준다.
Batch Normalization이 필요한 이유
딥러닝 모델을 훈련시키는 것은 마치 여러 층으로 이루어진 복잡한 파이프라인을 통해 물을 흘려보내는 것과 비슷하다. 이 과정에서 몇 가지 문제가 발생할 수 있다:
불안정한 물의 흐름: 데이터(물)가 네트워크를 통과하면서 그 분포가 계속 변하면, 각 층(파이프)은 계속 새로운 상황에 적응해야 한다. 이를 “Internal Covariate Shift”라고 부른다.
파이프 막힘 현상: 특정 활성화 함수(예: sigmoid)를 사용할 때, 데이터가 0에 가까워지면서 흐름이 거의 멈추는 “기울기 소실(gradient vanishing)” 문제가 발생할 수 있다.
미세 조정의 어려움: 학습률(learning rate)과 같은 설정값을 조절하는 것이 매우 까다롭다. 잘못 설정하면 학습이 제대로 되지 않거나 발산할 수 있다.
Batch Normalization은 이러한 문제들을 해결하기 위해 제안되었다.
Batch Normalization의 핵심 아이디어
Batch Normalization의 핵심 아이디어: “데이터의 분포를 일정하게 유지하자!”
구체적으로, 다음과 같은 과정을 거친다:
- 정규화(Normalize): 각 특성(feature)의 평균을 0, 분산을 1로 만든다.
- 스케일 조정과 이동: 정규화된 값에 학습 가능한 파라미터를 곱하고 더한다. 이를 통해 모델의 표현력을 유지한다.
수식으로 표현하면 다음과 같다:
- $\hat{x} = \frac{x - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}$ (정규화)
- $y = \gamma \hat{x} + \beta$ (스케일 조정과 이동)
여기서 $\mu_B$와 $\sigma_B^2$는 미니배치의 평균과 분산, $\gamma$와 $\beta$는 학습 가능한 파라미터, $\epsilon$은 0으로 나누는 것을 방지하기 위한 작은 값이다.
Batch Normalization의 장점
- 안정적인 학습: 데이터 분포를 일정하게 유지하여 학습을 안정화한다.
- 높은 학습률 사용 가능: 기울기 폭발 문제를 완화하여 더 높은 학습률을 사용할 수 있게 한다.
- 초기화에 덜 민감: 가중치 초기화에 덜 민감해져 학습 시작이 쉬워진다.
- 규제(Regularization) 효과: 미니배치 단위로 정규화하므로 약간의 노이즈가 추가되어 과적합을 방지한다.
실제 적용 예시
- MNIST 손글씨 인식:
- Batch Normalization을 적용한 모델이 더 빠르게 학습하고 높은 정확도를 달성했다.
- ImageNet 대규모 이미지 분류:
- Inception 모델에 Batch Normalization을 적용하여 학습 시간을 14배 단축하고, 더 높은 정확도를 달성했다.
- Sigmoid 활성화 함수를 사용해도 학습이 가능해졌다 (이전에는 거의 불가능했음).
- 앙상블 모델:
- Batch Normalization을 적용한 모델들로 앙상블을 구성하여 당시 ImageNet 대회에서 최고 성능을 달성했다.
결론
- 학습 속도를 크게 높힌다.
- 모델의 안정성을 개선한다.
- 별도의 복잡한 기법 없이도 모델의 일반화 성능을 높여준다.
Batch Normalization의 도입으로, 이전에는 학습이 어려웠던 깊고 복잡한 네트워크도 효과적으로 학습할 수 있게 되었다. 현재 대부분의 딥러닝 모델에서 기본적으로 사용되는 필수적인 기법이 되었다.
원본
핵심 요약
- 딥러닝 모델 훈련시 가장 보편적으로 사용되고 있는 Batch Normalization 기법을 제시한 논문이다.
- 높은 학습률에도 안정적이고, dropout 없이도 모델을 Regularization 한다.
Introduction
딥러닝 모델에서 사용하는 SGD 는 미니배치를 사용해 전체 훈련데이터의 gradient 를 추정할 수 있다. 또한, batch 단위 계산을 병렬적으로 수행할 수 있어 계산 효율성 또한 높일 수 있다.
그러나 SGD 는 learning rate 등의 hyperparameter 와 초기값에 민감하여 세밀한 조정이 필요하다. 잘못된 셋팅으로 인해 생긴 악영향은 레이어를 거치면서 증폭될 수 있다.
특히 Input 데이터의 분포가 변하게 되는 경우, 학습을 진행하면서 계속 새로운 분포에 적응을 해야하게 된다. 이러한 문제를 covariate shift 라고 부른다.
이렇게 Input 분포가 변화할 때 딥러닝 모델 내부 layer 의 출력 분포도 변한다면, 이를 Internal Covariate Shift 라고 정의한다. 이 현상은 sigmoid 함수 등을 사용했을 때 activation 이 0 에 수렴하게 되는 gradient vanishing 문제를 야기할 수 있다. 또한 학습 속도를 늦춰 모델에 전반적인 악영향을 끼친다.
논문은 Internal covariate shift를 해결하기 위한 Batch Normalization 이라는 방법을 제안한다. 이는 각 레이어의 인풋값들의 평균과 분산을 고정시킴으로써 Internal covariate shift를 감소시키고, 딥러닝 네트워크의 학습속도을 개선할 수 있다. 논문은 또한 다음과 같은 장점을 제시한다.
- 학습 파라미터의 스케일과 초기값에 대한 의존성을 감소
- 발산의 위험 없이 더 높은 러닝레이트를 사용 가능
- dropout과 같은 기법을 사용하지 않고도 regularizer 역할을 수행
- saturated mode에 빠질 위험성을 제거하여 saturating nonlinearities (sigmoid, tanh) 등 사용 가능
Towards Reducing Internal Covariate Shift
Input 데이터 분포의 상관관계를 제거하고, 평균을 0으로 하고 단위 분산을 갖도록 선형변환할 때, 네트워크가 더 빨리 수렴한다고 알려져 있다.
때문에 매 step/interval 마다 activation whitening 을 수행하도록 모델 구조를 변경할 수도 있다. 그러나, whitening 변환이 최적화 단계에 포함되지 않는 경우, normalization 값이 업데이트 되어야만 파라미터를 업데이트할 수 있기에, gradient 효과를 감소시키게 된다.
이를 해결하기 위해서는 네트워크가 항상 원하는 분포의 activation 을 생성하도록 설계해야한다. 단, 이러한 normalization 방식은 covariate matrix 와 back-prop gradient 등 expensive 계산을 요구한다. 따라서, 논문은 미분가능한 동시에 전체 학습데이터가 아닌 일부 데이터만으로도 수행가능한 normalization 방법을 찾으려 한다.
Normalization via Mini-Batch Statistics
모든 layer 의 입출력을 결합하여 whitening 하는 대신, 각 feature 가 독립적이라고 가정하며 normalization 을 수행한다.
이때, 단순한 normalization 을 수행하면, layer 의 표현력이 변할 수 있다. 때문에, 아래와 같이 scale과 shift를 포함하는 선형 변형을 수행한다. $\gamma$ 와 $\beta$ 는 모델 파라미터와 동시에 학습하는 파라미터이다.
또한, stochastic optimization 을 가정하고, mini batch 를 기반으로 평균과 분산 을 계산한다.
위 과정을 정리함녀 아래와 같은 batch normalizing transform 알고리즘을 정의할 수 있다.
이는 본래 논문이 목표한 바와 같이 미분가능한 변환이며, 네트워크에 normalized 된 activation 을 제공한다.
Training and Inference with Batch-Normalized Networks
Training 이 아닌 Inference 상황에서도 Batch Normalization 을 적용하기 위한 방법을 설명한다. 학습때와 같이 mini-batch를 사용하는 것이 아닌, 학습과정에서 얻은 미니배치들의 평균, 분산으로 “unbiased” mean/variance estimator를 계산하여 사용한다. 이를 정리하면 아래와 같다.
Batch-Normalized Convolutional Networks
Batch Normalization을 Convolution layer 에 적용할 수 있는 방법을 설명한다. Conv layer 는 BN을 수행하고도 convolution 의 성질을 유지해야한다, 따라서, mini batch 의 모든 위치에서의 activation 전체를 사용해 normalization 한다.
Batch Normalization enables higher learning rates
BN layer 는 activation 을 normalization 함으로서, 가중치의 변화가 layer 를 거치며 증폭되는 현상을 막는다. 따라서, gradient vanishing 과 exploding 을 모두 방지할 수 있다. 이는 더 높은 learning rate 를 사용해 빠른 학습을 유도할 수 있음을 의미한다.
Batch Normalization regularizes the model
학습 시 BN layer는 어떤 한 data sample만이 아니라 mini-batch 내의 다른 data sample들도 고려하여 normalization을 수행한다. 따라서, 해당 data sample에 deterministic한 결과를 생성해내지 않으므로 model regularization 효과 또한 제공한다.
Experiments
Activations over time
MNIST 데이터셋을 사용하여 실험을 진행합니다. 학습에 사용한 모델은 다음과 같다.
- 3 fully connected layer, 100 activation
- sigmoid 활성함수
- cross-entropy loss 사용
- 50000 epoch 학습
- batch size 60
- BN 을 사용한 모델과 사용하지 않은 모델로 구분
Batch Normalization 을 추가했을 때 더 높은 모델 성능을 보임을 제시한다. 또한, Internal covariate shift 도 감소시켰음을 보인다.
ImageNet classification
Imagenet 데이터로 Inception 모델을 사용하여 실험을 진행했음을 언급한다.
Accelerating BN Networks
단순히 BN 을 추가한 것만으로는 모델 성능 개선이 어려웠음을 언급하며, 개선한 실험 셋팅을 설명한다.
Single-Network Classification
LSVRC2012 훈련/검증/테스트 데이터를 사용하여 아래와 같은 단일 신경망 모델로 학습한 결과를 비교하여 제시한다.
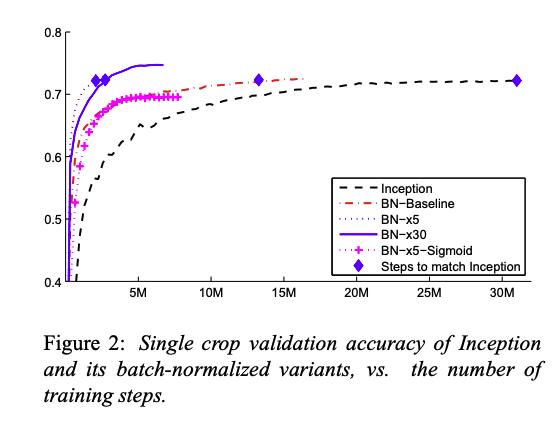
BN-Baseline 모델만으로도 절반의 훈련시간으로 Inception 모델의 정확도를 달성했음을 언급한다.
BN-x5 는 14배 빠른 속도와 더 높은 성능을 보인다. 또한 BN 을 사용함으로서 Sigmoid last layer 를 사용한 경우에도 학습이 가능했음을 언급한다.
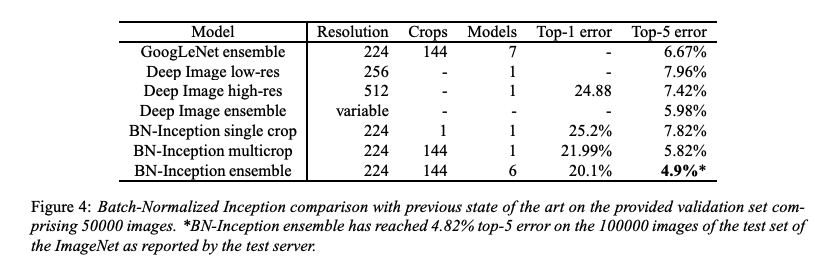
Ensemble Classification
BN-x30 모델 6개로 ensemble 을 수행하여 ImageNet SOTA 를 달성한 결과를 제시한다.
Conclusion
covariate shift 를 제거하고 딥러닝 모델 학습 속도를 개선할 수 있는 Batch Normalization 방법을 소개한다.
Dropout 을 사용하지 않고도 Regularization 효과를 보였으며, ImageNet 에서 SOTA 를 달성하였다.