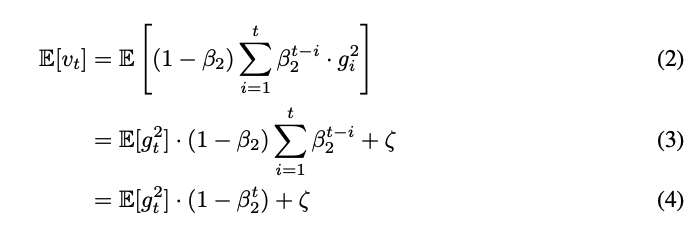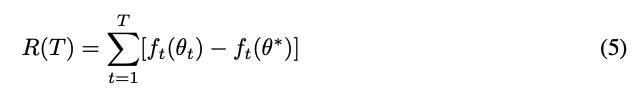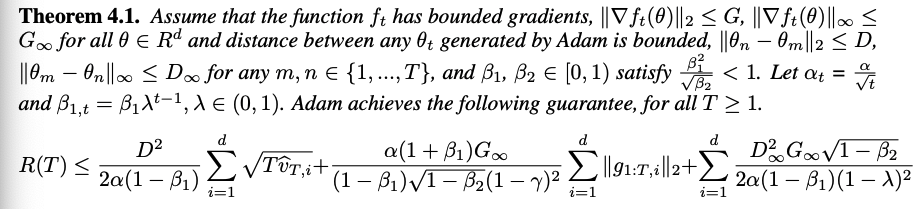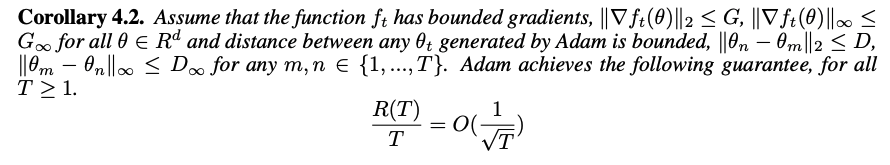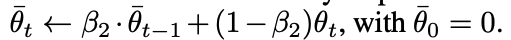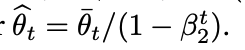Adam 논문 리뷰
| 태그 | #Training |
|---|---|
| 한줄요약 | Adam |
| Journal/Conference | #ICLR |
| Link | Adam |
| Year(출판년도) | 2015 |
| 저자 | Diederik P. Kingma, Jimmy Ba |
| 원문 링크 | Adam |
쉬운 설명
핵심 요약
Adam(Adaptive Moment Estimation)은 딥러닝 모델을 훈련할 때 널리 사용되는 최적화 알고리즘이다.
- Adam은 Momentum과 RMSprop 두 가지 인기 있는 방법의 장점을 결합했다.
- 데이터가 불규칙하거나 희소해도 안정적으로 학습할 수 있다.
- 학습 속도(learning rate)를 자동으로 조절하여 빠르게 최적의 결과에 도달한다.
쉽게 말해, Adam은 딥러닝 모델이 더 빠르고 안정적으로 배울 수 있도록 도와주는 알고리즘이다.
왜 Adam이 필요한가?
딥러닝 모델을 훈련시키는 것은 마치 안개 낀 울퉁불퉁한 산을 오르는 것과 비슷하다. 목표는 가장 높은 곳(최적의 성능)에 도달하는 것이다. 이 과정에는 여러 가지 어려움이 있다:
- 불규칙한 지형: 데이터가 불규칙하거나 노이즈가 많으면, 마치 울퉁불퉁한 지형을 오르는 것과 같다.
- 안개 낀 날씨: 전체 데이터의 일부만 사용하여 학습하므로, 전체 지형을 다 볼 수 없는 것과 같다.
- 적절한 보폭 선택: 너무 크게 걸으면 넘어질 수 있고, 너무 작게 걸으면 정상에 도달하는 데 오래 걸린다.
Adam은 이러한 문제들을 해결하기 위해 고안되었다.
Adam의 핵심 아이디어
Adam은 세 가지 주요 기술을 결합한다:
- Momentum: 과거의 “움직임”을 기억하여 활용
- RMSprop: 각 파라미터마다 다른 보폭(학습률) 사용
- Bias Correction: 초기 학습 단계에서의 불안정성 보정
이 세 가지 요소가 어떻게 작동하는지 자세히 살펴보면
1. Momentum
수식: $m_t = \beta_1 \cdot m_{t-1} + (1-\beta_1) \cdot g_t$
설명:
- 이것은 “관성”의 개념과 비슷하다.
- 공이 굴러가듯이, 이전에 움직이던 방향으로 계속 움직이려는 경향을 나타낸다.
왜 중요한가?:
- 학습 과정에서 지그재그로 움직이는 것을 줄여준다.
- 특히 ‘협곡’ 같은 지형에서 유용하다. 협곡의 양쪽 벽면을 왔다갔다 하는 대신, 협곡의 바닥을 따라 더 빠르게 내려갈 수 있게 해준다.
2. RMSprop (Root Mean Square Propagation)
수식: $v_t = \beta_2 \cdot v_{t-1} + (1-\beta_2) \cdot g_t^2$
설명:
- 각 파라미터가 얼마나 자주, 크게 변하는지 추적한다.
- 자주 변하는 파라미터는 작은 보폭으로, 덜 변하는 파라미터는 큰 보폭으로 조정한다.
왜 중요한가?:
- 모든 파라미터를 동일하게 취급하지 않고, 각각에 맞는 “맞춤형” 학습률을 제공한다.
- 이를 통해 어떤 파라미터는 빠르게, 어떤 파라미터는 천천히 학습할 수 있게 된다.
3. Bias Correction
수식: $\hat{m}_t = m_t / (1-\beta_1^t)$ $\hat{v}_t = v_t / (1-\beta_2^t)$
설명:
- 학습 초기에 발생할 수 있는 “편향”을 보정한다.
- 마치 처음 등산을 시작할 때 조심스럽게 걸음을 옮기는 것과 비슷하다.
왜 중요한가?:
- 학습 초기부터 안정적인 업데이트가 가능해진다.
- 잘못된 방향으로 크게 움직이는 것을 방지한다.
최종 업데이트 규칙
수식: $\theta_t = \theta_{t-1} - \alpha \cdot \hat{m}_t / (\sqrt{\hat{v}_t} + \epsilon)$
설명:
- 이 수식은 실제로 모델의 파라미터를 어떻게 업데이트할지 결정한다.
- Momentum (관성)과 적응적 학습률을 모두 고려하여 각 파라미터를 조정한다.
왜 중요한가?:
- 각 파라미터마다 “똑똑하게” 스텝 크기를 조절한다.
- 빠르게 변해야 하는 파라미터는 큰 스텝으로, 천천히 변해야 하는 파라미터는 작은 스텝으로 업데이트된다.
Adam의 장점
- 안정성: 불규칙한 데이터에서도 안정적으로 학습할 수 있다.
- 효율성: 학습 속도를 자동으로 조절하여 빠르게 최적의 결과에 도달힌다.
- 메모리 효율: 추가적인 메모리를 많이 사용하지 않는다.
- 직관적인 해석: 하이퍼파라미터(학습에 영향을 주는 설정값들)의 의미를 이해하기 쉽다.
실제 적용 예시
- 이미지 인식:
- MNIST 데이터셋(손으로 쓴 숫자 이미지)을 사용한 실험에서 Adam은 다른 방법들보다 빠르게 학습했다.
- 예: 100번의 반복(iteration) 후 Adam은 98% 정확도에 도달했지만, 기본 SGD는 95%에 머물렀다.
- 자연어 처리:
- IMDB 영화 리뷰 데이터를 사용한 감성 분석에서도 Adam은 효과적이었다.
- 예: 10,000개의 고유 단어를 사용한 분류 작업에서, Adam은 50 에폭(epoch) 만에 최고 성능에 도달했지만, SGD는 100 에폭 이상 걸렸다.
- 복잡한 신경망:
- 여러 층으로 이루어진 신경망이나 합성곱 신경망(CNN)에서도 Adam은 우수한 성능을 보였다.
- 예: 5층 신경망에서 Adam은 각 층마다 다른 학습률을 자동으로 적용하여, 전체적인 학습 속도를 크게 향상시켰다.
결론
- Momentum을 통해 일관된 방향으로 학습한다.
- RMSprop을 통해 각 파라미터에 맞는 학습률을 제공한다.
- Bias correction을 통해 초기 학습을 안정화한다.
실제 사용시 주로 세 가지 하이퍼파라미터($\alpha$, $\beta_1$, $\beta_2$)만 조정하면 되므로 사용이 간편하다. 대부분의 경우 기본값($\alpha=0.001$, $\beta_1=0.9$, $\beta_2=0.999$)으로도 좋은 성능을 보인다.
Adam은 다양한 상황에서 안정적이고 효율적으로 작동하여, 현재 가장 널리 사용되는 최적화 알고리즘 중 하나이다.
원본
핵심 요약
- Momentum과 Adagrad 를 종합한 Adam(Adaptive Moment Estimation) optimizer를 제시한다.
- Gradient가 Noisy 하거나 sparse 한 경우에도 학습을 안정적으로 수행한다.
- 2개의 hyperparameter 만으로, learning rate의 범위 안에서 stepsize 를 스스로 조정하여 빠르게 수렴한다.
Introduction & Related Work
SGD(Stochastic Gradient Descent) 는 전체 데이터 중 일부를 batch로 사용해 목적 함수를 계산하므로, 동일한 데이터로 같은 step 만큼 학습한 경우에도 목적 함수(Objective function)의 값이 달라질 수 있다. 이와 유사하게, Dropout은 랜덤하게 node를 drop 시켜 서로 다른 모델들을 학습해나가므로 최종 목적 함수의 값이 다를 수 있다. 이처럼, 머신러닝의 목적 함수는 다양한 노이즈로 인해 확률적 (stochastic)으로 변화할 수 있다.
Adam(Adaptive moment estimation) 은 기존 SGD 기반 최적화 알고리즘의 주요 아이디어를 조합한 효율적인 최적화 알고리즘이다.
- Momentum : gradient의 1st moment 로 파라미터를 업데이트
- Adagrad : gradient의 2nd moment를 사용하며, weight 별로 Adaptive 하게 Gradient를 계산
- RMSProp : decay rate를 사용해 moment 의 지수 이동 평균을 계산
Adagrad는 학습을 지속할수록 step size가 감소하여 학습이 완료되지 않은 경우에도 step size가 0에 수렴할 수 있다. RMSProp with Momentum은 decay rate에 따라서 step size가 발산할 수 있다. 이를 해결하기 위해 Adam 은 bias correction 과정을 통해 moment의 비편향 추정(unbiased estimate)을 계산한다.
구체적으로 Adam은 1st-order gradient의 비편행 평균 / 분산 추정(Unbiased 1st / 2nd moment estimate)을 사용해 모델 파라미터를 업데이트 한다. 따라서, gradient 의 크기에 관계없이 step size를 일정한 크기로 bound 하므로 안정적인 학습이 가능하다.
Algorithm
위는 Adam의 pseudo 코드로, 아래와 같이 정리할 수 있다.
- 초기 파라미터 제기 (hyperparameter: $\alpha$, $\beta_1$, $\beta_2$ / 모델 $\text{parameter}$)
- $\text{moment}$ 초기값 제시 ($m_0$, $v_0$ = 0)
- 1st-order gradient의 biased 1st / 2nd moment estimate 계산 ($m_t$, $v_t$)
- bias correction 으로 unbiased 1st / 2nd moment estimate 계산 ($\hat{m}_t$, $\hat{v}_t$)
- 모델 parameter update($\hat{m}_t$, $\sqrt{\hat{v}_t}$)
biased moment estimate 는 1st order gradient $g_t$ 의 지수이동평균이며, $\beta$ 를 사용하여 지수이동평균 계산 과정의 가중치를 조정한다. $\beta$ 는 decay rate 라고 부르는 hyperparameter 로, 학습률 $\alpha$ 또한 아래와 같이 $\beta$ 를 사용해 조정할 수 있다.
\[\alpha_t = \alpha \cdot \sqrt {1-\beta_2^t}/(1-\beta_1^t)\text{ and }\theta_t \leftarrow \theta_{t-1} - \alpha_t \cdot m_t / (\sqrt{v_t} + \hat{\epsilon})\]Adam 의 1st moment estimate $m_t$ 는 Momentum 알고리즘, 2nd moment estimate $v_t$ 는 AdaGrad/RMSProp 알고리즘의 계산 방식과 동일하다. 이 때, $m_0$, $v_0$ 를 0으로 초기화했기때문에 학습 초기에는 $m_t$, $v_t$ 의 값이 0으로 편중(bias)된다. bias correction 작업은 이러한 bias 를 제거하고 올바른 1st/2nd moment 추정을 제공한다.
Adam’s Update Rule
Adam 의 가장 중요한 특성은 스스로 적절한 stepsize 를 조정할 수 있다는 점이다. 먼저, noise 가 없는 경우의 effective stepsize 를 $\Delta t = \alpha \cdot \hat{m_t}/\sqrt{\hat{v_t}}$ 라고 정의한다. effective stepsize 는 $\alpha$, $\beta$ 의 값에 따라 아래와 같이 크기가 제한된다.
\[|\Delta_t| \le \begin{cases} \alpha \cdot (1-\beta_1)/\sqrt{1-\beta_2} & (1-\beta_1)>\sqrt{1-\beta_2} \\ \alpha & otherwise \end{cases}\]위의 경우는 현재의 gradient 를 제외한 이전 timestep 의 gradient 가 모두 0인 극단적인 경우에만 성립하며, 대부분의 경우 stepsize 는 $\alpha$ 로 제한된다.
여기에 더해 optimum 에 가까워질수록, 현재 향하고 있는 gradient 방향의 불확실성이 커지므로($\hat{v_t}$ 증가), $\hat{m_t}/\sqrt{\hat{v_t}}$ 가 0에 가까워진다. 또한, $\hat{m_t}/\sqrt{\hat{v_t}}$ 는 gradient 의 크기에 영향을 받지 않는다.
따라서 Adam 은 $\alpha$ 범위 안에서 학습을 진행해감에 따라 effective stepsize 를 스스로 조정할 수 있다.
Initialization Bias Correction
앞서 구한 ($m_t, v_t$) 는 gradient 의 1st/2nd moment 에 대한 편향된(biased) 추정이라고 언급하였다.
즉, 2nd moment 로 예로 들었을 때, 실제 gradient 의 2nd moment $\mathbb{E}[g_t^2]$ 는 $\mathbb{E}[v_t]$ 와 값이 달라진다. Adam 은 실제 gradient 의 moment 를 구하기 위한 bias correction 과정을 통해 비편향 추정(unbiased estimate)을 구한다.
먼저, $v_0 = 0, v_t = \beta_2 \cdot v_{t-1} + (1-\beta_2) \cdot g_t^2$ 의 점화식을 풀면 아래와 같은 식을 얻을 수 있다.
\[v_t = (1-\beta_2) \sum_{i=1}^t \beta_2^{t-i} \cdot g_i^2\]다음으로 양변에 기대값을 취해주면 아래와 같이 실제 2nd moment 와의 차이를 구할 수 있다.
결과적으로, $\hat{v_t} = v_t / (1-\beta_2^t)$ 와 같이 $\mathbb{E}[\hat{v_t}] = \mathbb{E} [g_t^2]$ 가 되도록 bias correction 을 수행한다. 이는 1st moment estimate $m_t$ 에서도 동일하다.
Convergence Analysis
Online learning 에 적용한 Adam 알고리즘이 실제로 최적 parameter 에 수렴할 수 있음을 증명한다.
먼저 “Regret” 은 아래 수식과 같이 정의되며, 모델의 최적값과 예측값의 차이를 누적하여 합한 값이다.
논문은 아래와 같이 Adam 의 regret bound 를 유도한다.
이 때, Adam 은 $O(\log d \sqrt{T})$ $의 bound 를 가지며, 이는 $O(\sqrt{dT})$ 의 bound 를 가지는 기존 non-adaptive learning 방법에 비해 더욱 빠르게 수렴할 수 있음을 의미한다. 결과적으로, Adam 의 Regret bound 는 아래와 같이 정리된다.
Experiments
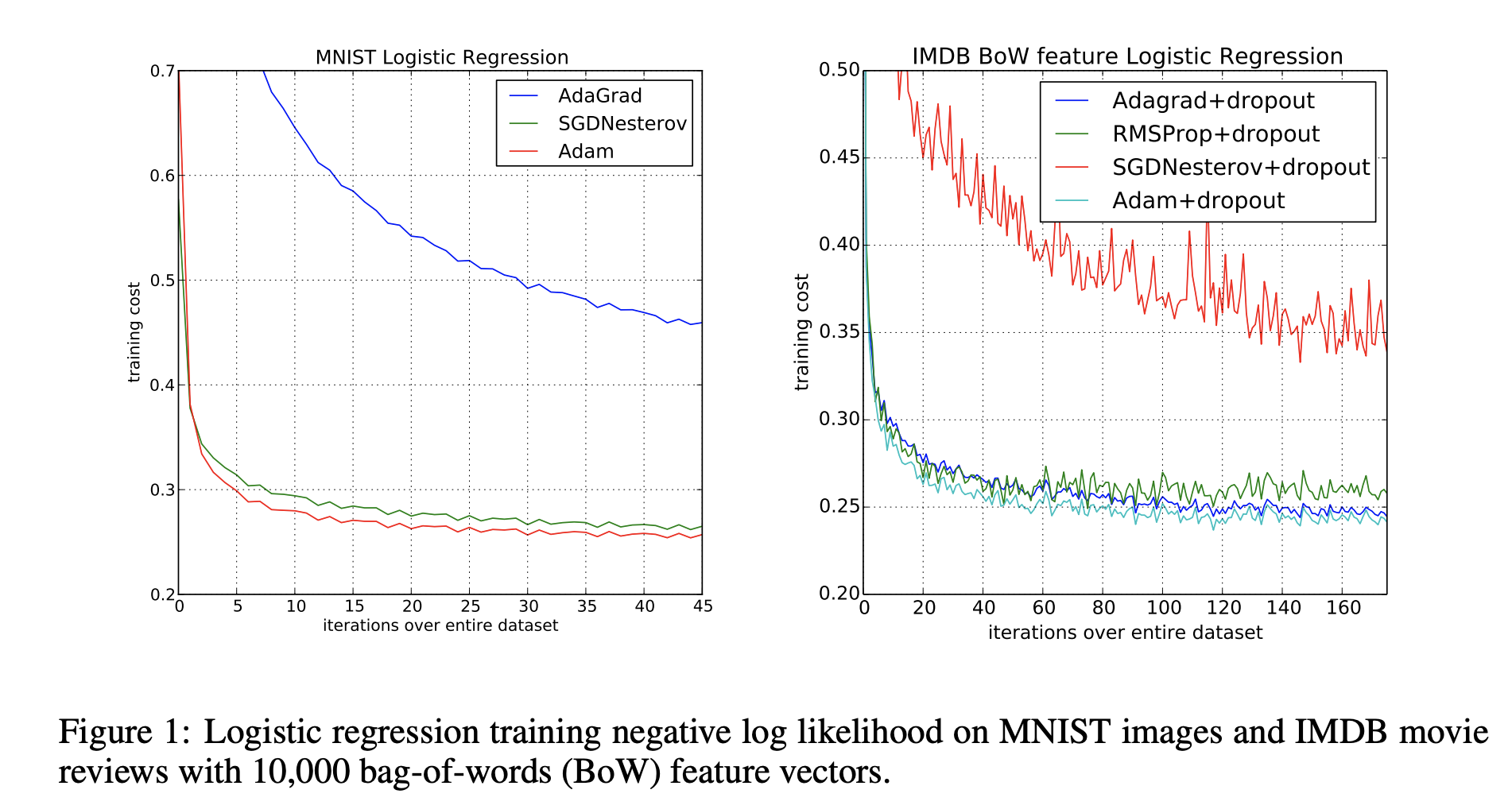
EXPERIMENT: LOGISTIC REGRESSION
아래 2 가지 데이터셋으로 logistic regression 을 수행하여 Adam, SGD(with Nesterov momentum), AdaGrad 를 비교한다.
- MNIST
- multi-class logistic regression
- $1/\sqrt{t}$ 에 따라 step size $\alpha$ 를 조정
- batch size : 128
- IMDB
- sparse feature problem - Bow(bag-of-words) Features vector (d=10000)
- 영화 리뷰에서 가장 빈번하게 보이는 10000 개 단어의 빈도를 벡터로 표현
- 50% dropout
- sparse feature problem - Bow(bag-of-words) Features vector (d=10000)
왼쪽의 MNIST 학습 결과에서는 momentum 이 적용된 알고리즘(Adam,SGD)이 그렇지 않은 경우(Adagrad)에 비해 빠르게 수렴하는 것을 확인할 수 있다. 반면 오른쪽의 IMBD 학습 결과에서는 Adagrad 등이 SGD 보다 sparse feature 에서 빠르게 수렴한다.
즉, Adam 은 momentum 을 적용한 알고리즘과 같이 일반적인 문제에서 빠르게 수렴하며, sprase feature 또한 원활하게 학습할 수 있다.
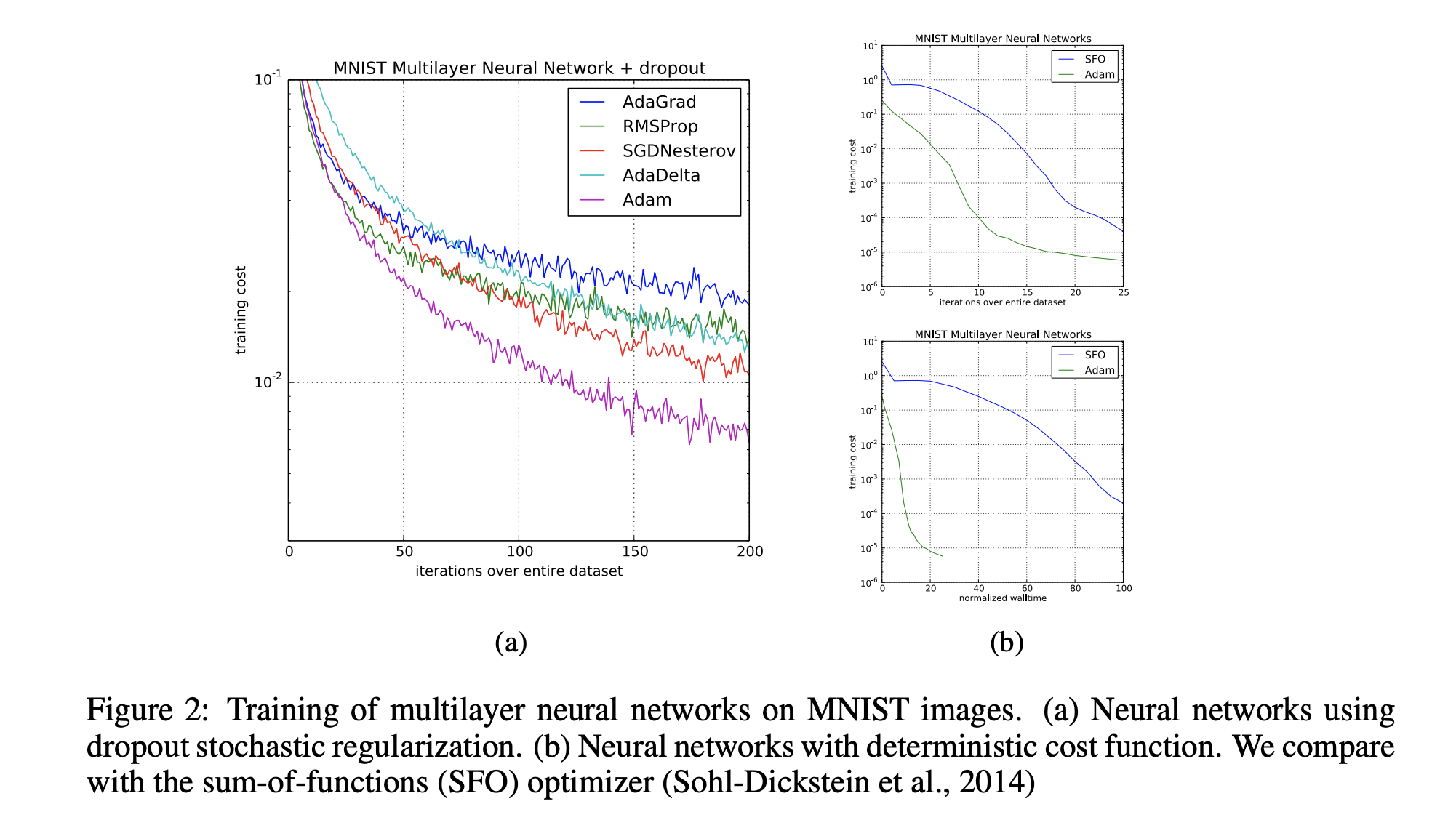
EXPERIMENT : MULTI-LAYER NEURAL NETWORKS
MNIST 데이터셋으로 다층 인공신경망에서의 성능을 확인
- 2 layer, d=1000
- ReLU 활성함수 사용
- batch size : 128
- Cross-Entropy loss, L2 weight decay 사용
Adam 은 dropout 을 적용하여 noisy 한 환경에서도 기존 stochastic optimization 알고리즘보다 빠르게 수렴하는 것을 확인할 수 있다.
또한, deterministic 한 환경에서도 iteration 횟수 및 실제 계산 시간 측면에서 기존 알고리즘(SFO)보다 월등히 빠른 수렴속도를 보여준다.
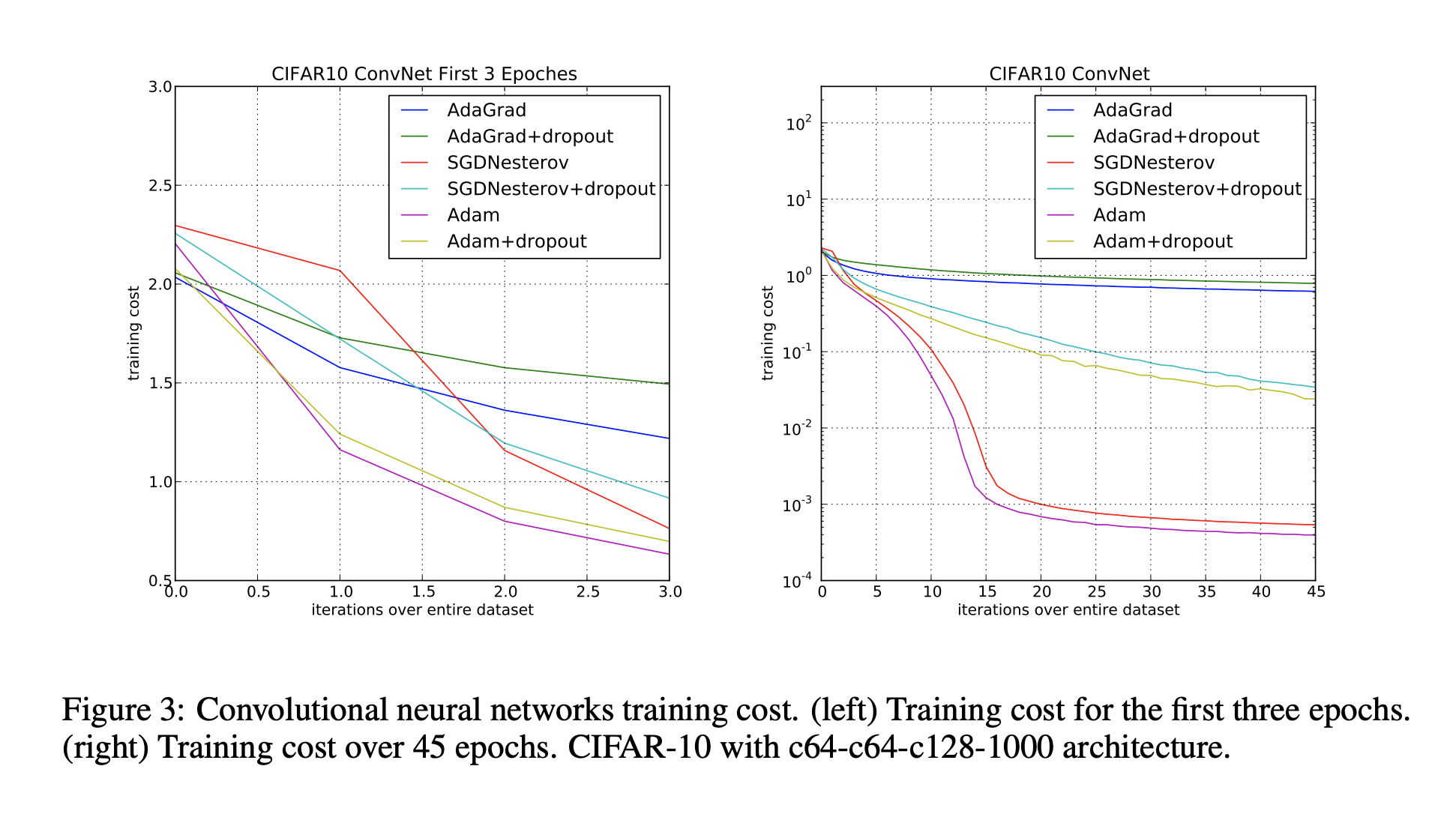
EXPERIMENT : CONVOLUTIONAL NEURAL NETWORKS
MNIST 데이터셋에서, 아래와 같은 CNN 모델로 Adam 의 성능을 확인
- 3 convolution layer
- 5x5 convolution
- 3x3 max pooling (stride=2)
- 1 fully connected layer (d=1000)
- ReLU 활성함수 사용
- batch size : 128
왼쪽과 같이 초기 학습단계에서 Adam 은 Adagrad 처럼 빠르게 cost 를 감소시킨다. 또한 오른쪽의 그래프처럼, 학습이 지속될수록 성능이 감소하는 Adagrad 에 비해 꾸준하게 빠른 수렴속도를 보인다.
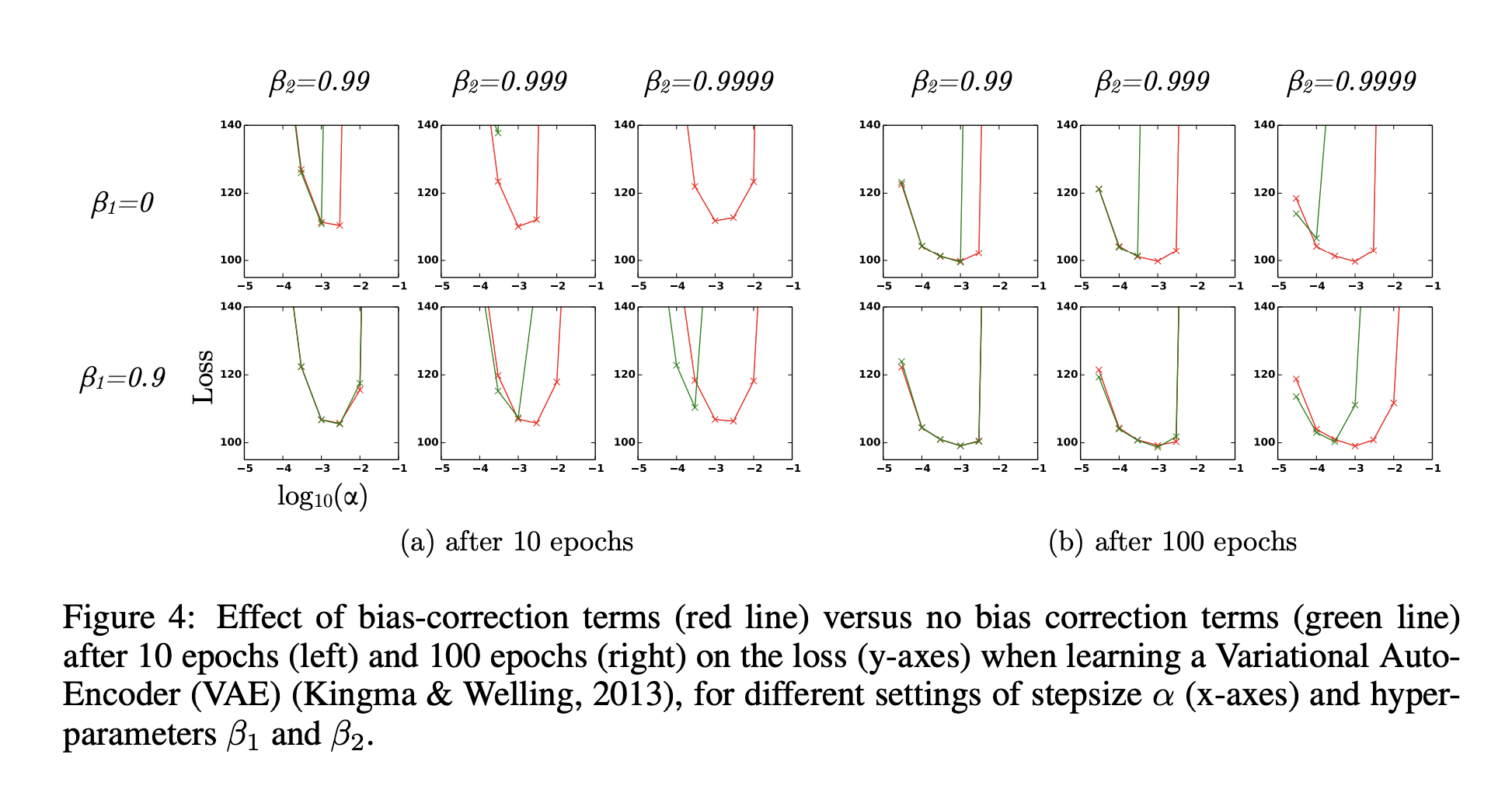
EXPERIMENT : BIAS-CORRECTION TERM
VAE 모델을 사용해, decay rate 를 조정하며 앞서 수행한 bias correction 의 효과를 검증한다.
- 1 layer (d=500)
- softplus
- gaussian latent variable (d=50)
학습을 진행할수록 특정한 pattern 을 학습한 모델의 gradient 는 sparse 하게 변한다. decay rate $\beta_2$ 는 1에 가까워질수록 초기 bias 를 강하게 주어 sparse gradient 문제를 효과적으로 풀 수 있게 한다. 그러나 강한 bias 를 correction 하지 않는다면 학습이 불안정해진다.
learning rate $\alpha$ 를 변경해가며 loss 값을 확인할 때, $\beta_2$ 가 1에 가까워질수록 bias correction을 수행하지 않은 경우(초록색)의 학습 불안정성이 커지는 것을 확인할 수 있다. 반면 bias correction 을 수행한 경우 높은 $\beta_2$ 에도 안정적으로 학습을 수행한다. 결과적으로 Adam 은 동일한 hyperparameter 가 주어진 경우에도 RMSProp(with momentum) 보다 안정적이고 더 좋은 성능을 보인다.
Experiments
ADAMAX
Adam 은 아래와 같이 과거 및 현재 gradient 의 $L^2$ norm ($g_i^2$) 을 사용하여, 각각의 weights 를 이에 반비례하게 조정한다.
\[v_t = (1-\beta_2) \sum_{i=1}^t \beta_2^{t-i} \cdot g_i^2\]이 때, 아래와 같이 $L^2$ norm 을 $L^p$ norm 으로 조정하면, stepsize 는 $v_t^{1/p}$ 를 따라 변화한다. 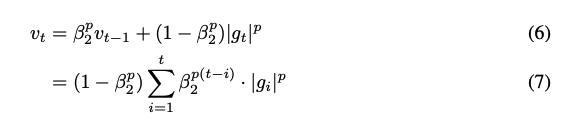
이 때, $p$ 값을 단순히 크게 하는 경우에는 알고리즘이 불안정해지지만, $p$ 가 무한대로 수렴하는 경우 아래와 같이 안정적인 알고리즘을 설계할 수 있다.
위의 AdaMax 알고리즘은 Adam 과 다르게 bias correction 없이도 수렴하며, decay rate 에 관계없이 step size 를 $\alpha$ 로 bound 한다.
TEMPORAL AVEREAGING
학습하고자 하는 모델 파라미터 $\theta$ 를 모든 step 에 대해 평균하여, iteration 을 진행할 수록 학습이 불안정해지는 현상을 보완할 수 있다. Adam 에도 아래와 같은 방법으로 이를 적용할 수 있다.
이 때, 다른 moment estimate 와 마찬가지로 bias correction 을 수행힌다.
CONCLUSION
Stochastic objective function 를 간단하고 효율적으로 최적화 할 수 있는 Adam 알고리즘을 제시한다.
Adam 은 Adagrad 처럼 weight 별로 step size 를 조정하여 sparse gradient 문제에 효과적이며, RMSprop 과 같이 momentum 을 사용하여 non-stationary objective 를 해결할 수 있다.