Post

2.1 머신러닝 주요 개념

Posted
By JUNHEE LEE
17 min read

2.1 머신러닝 주요 개념




분류와 회귀 분류 평가지표--
회귀 평가 지표 오차행렬
(정확도, 정밀도, 재현율, F1 점수)		로그 손실ROC
AUC


데이터 인코딩 피처 스케일링 교차검증 
레이블 인코딩원-핫 인코딩min-max 정규화표준화K 폴드층화 K 폴드


   주요 머신러닝 모델   
선형 회귀로지스틱 회귀결정 트리앙상블랜덤 포레스트XGBoostLightGBM


 하이퍼파라미터 최적화 
그리드서치랜덤서치베이지안 최적화




1. 분류와 회귀

  • 타겟값이 범주형 데이터이면 분류 문제, 수치형 데이터면 회귀 문제.


1.1 분류

  • 분류란 어떤 대상을 정해진 범주에 구분해 넣는 작업.

  • 머신러닝에서 분류는 주어진 feature에 따라 어떤 대상을 유한한 범주(타겟값)로 구분하는 방법.

  • target 값이 두개인 분류를 이진분류(binary classification), 세 개 이상인 분류를 다중분류(multiclass classification) 라고 한다.



1.2 회귀

자연현상이나 사회 현상에서 변수 사이에 관계가 있는 경우, 예를 들어, 학습 시간이 시험 성적에 매치는 영향, 수면의 질이 건강에 미치는 영향, 공장의재고 수준이 회사 이익에 미치는 영향 등.

이때 영향을 미치는 변수를 독립변수 라 하고, 영향을 받는 변수를 종속변수 라고 한다.

위 예시에서 학습 시간, 수면의 질, 공장의 재고 수준이 독립변수. 시험 성적, 건강, 회사 이익이 종속변수이다.

  • 회귀란 독립변수와 종속변수 간 관계를 모델링 하는 방법이다.

  • 회귀가 분류와 다른점은 종속변수(타겟값)가 범주형 데이터가 아니라는것, 회귀 문제에서 종속변수는 수치형 데이터.

\(Y = \theta_0 + \theta_1x\) 위 식처럼 독립변수 하나($x$)와 종속변수 하나 ($Y$) 사이의 관계를 나타낸 모델링 기법을 단순 선형 회귀 라고 한다.

\(Y=\theta_0 + \theta_1x_1 + \theta_2x_2 + \theta_3x_3\) 위 식처럼 독립변수 여러개와 종속변수 하나 사이의 관계를 나타낸 모델링 기법을 다중 선형 회귀 라고 한다.

회귀 문제에서는 주어진 독립변수(feature)와 종속변수(타겟값) 사이의 관계를 기반으로 최적의 회귀계수를 찾아야 한다. 위 식에서 회귀계수(regression coefficient) 는 $\theta_1 \sim \theta_3$ 이다.


회귀 평가지표

회귀계수를 구하려면 예측값 실젯값의 차이, 즉 오차를 최소화해야 한다.

자주 이용하는 회귀 평가지표

회귀 평가지표수식설명
MAE${1\over N} \Sigma^{N}_{i=1} \mid y_i - \hat{y} \mid$평균 절대 오차 Mean Absolute Error.
실제 타겟값과 예측 타겟값 차의 절대 평균
MSE${1\over N} \Sigma^N_{i=1} (y_i - \hat{y})^2$평균 제곱 오차 Mean Squared Error.
실제 타겟값과 예측 타겟값 차의 제곱의 평균
RMSE$\sqrt{ {1\over N}\Sigma ^N_{i=1}(y_i - \hat{y})^2 }$평균 제곱근 오차 Root Mean Squared Error.
MSE에 제곱근을 취한 값
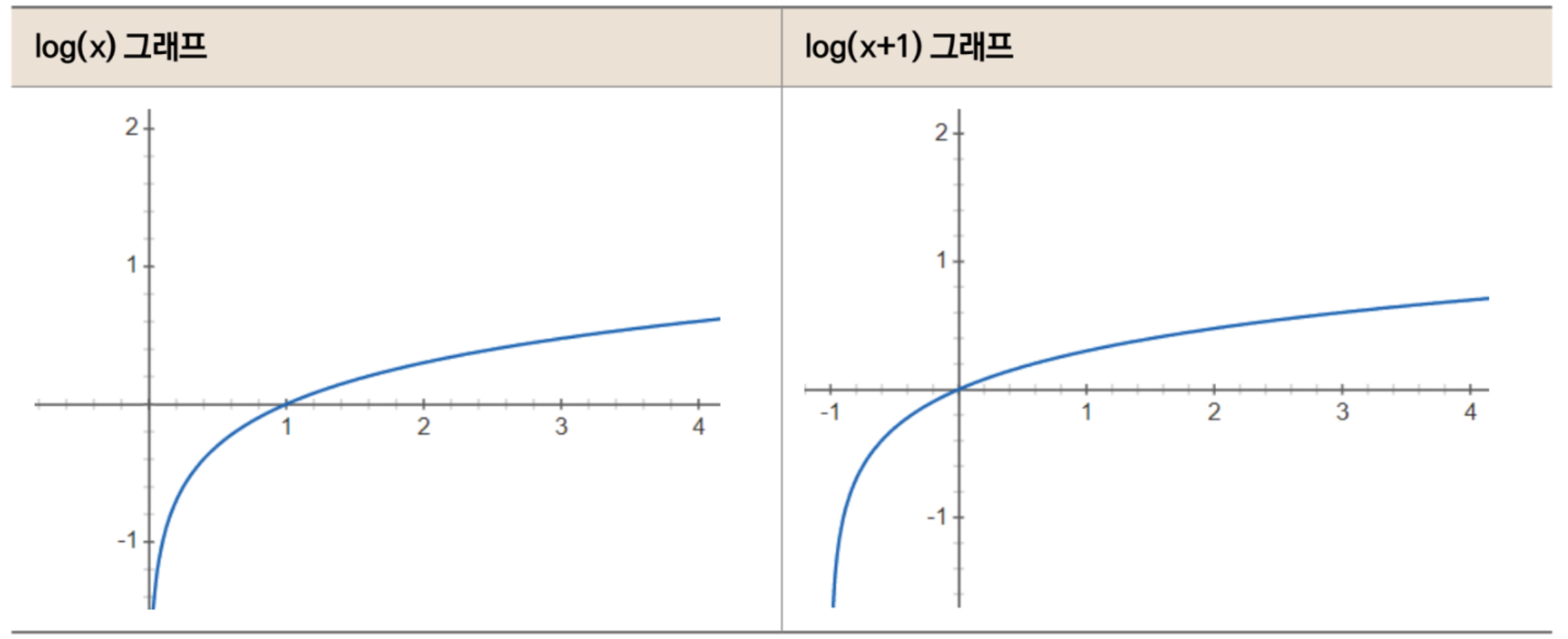
MSLE${1\over N}\Sigma^N_{i=1}(log(y_i + 1) - log(\hat{y_i} + 1))^2$Mean Squared Log Error.
MSE 에서 타겟값에 로그를 취한 값
RMSLE$\sqrt{ {1\over N}\Sigma^N_{i=1} (log(y_i + 1) - log(\hat{y}_i + 1))^2 }$Root Mean Squared Log Error.
MSLE에 제곱근을 취한 값
$R^2$$\hat{\sigma}^2\over{\sigma}^2$결정계수. 에측 타겟의 분산 / 실제 타겟값의 분산

*다른 지표들과 다르게 1에 가까울수록 모델 성능이 좋음



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

import numpy as np

# MAE, MSE, MSLE, R2
from sklearn.metrics import mean_absolute_error, mean_squared_error, mean_squared_log_error, r2_score

true = np.array([1, 2, 3, 2, 3, 5, 4, 6, 5, 6, 7, 8, 8])  # y_true
preds = np.array([1, 1, 2, 2, 3, 4, 4, 5, 5, 6, 6, 6, 8]) # y_hat

MAE = mean_absolute_error(true, preds)
MSE = mean_squared_error(true, preds)
RMSE = np.sqrt(mean_squared_error(true, preds))
MSLE = mean_squared_log_error(true, preds)
RMSLE = np.sqrt(mean_squared_log_error(true, preds))
R2 = r2_score(true, preds)

print(f'MAE:\t {MAE:.4f}' )
print(f'MSE:\t {MSE:.4f}')
print(f'RMSE:\t {RMSE:.4f}')
print(f'MSLE:\t {MSLE:.4f}')
print(f'RMSLE:\t {RMSLE:.4f}')
print(f'R2:\t {R2:.4f}')


"""
MAE:	 0.5385
MSE:	 0.6923
RMSE:	 0.8321
MSLE:	 0.0296
RMSLE:	 0.1721
R2:	     0.8617
"""



상관계수

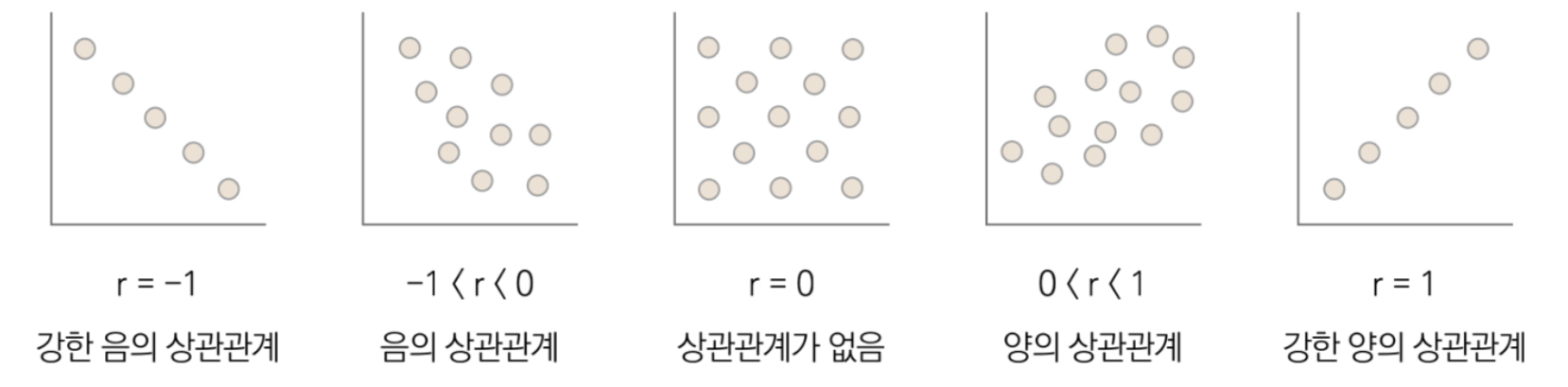
  • 두 변수 사이의 상관관계 (correlation) 정도를 수치로 나타낸 값을 상관계수 (correlation coefficient) 라고 한다.

  • 상관계수는 보통 약자 r로 표기한다.

  • 가장 많이 쓰는 선형 회귀 상관계수는 피어슨 상관계수이다.

  • 피어슨 상관계수는 선형 상관관계의 강도와 방향을 타나내며 -1 부터 1 사이의 값을 갖는다.

  • 상관계수가 음수면 음의 상관관계가 있다고 하고, 양수면 양의 상관관계가 있다고 한다.





2. 분류 평가지표

2.1 오차 행렬

  • 오차행렬은 실제 타겟값과 예측한 타겟값이 어떻게 매칭되는지를 보여주는 표이다. 혼동 행렬이라고도 한다.

  • 실제 타겟값이 양성인데 예측도 양성으로 했다면 True Positive이고 실제 타겟값은 양성인데 예측을 음성으로 했다면 False negative 이다.

  • 실제 타겟값이 음성인데 예측을 양성으로 했다면 False Positive 이고, 실제 타겟값이 음성인데 예측도 음성으로 했다면 True Negative이다.

  • 네 가지 경우를 표 형태로 나타낸 것을 오차 행렬 이라고 한다.

T로 시작하면 올바르게 예측한것이고 F로 시작하면 틀렸다는 뜻

  • 오차 행렬을 활용한 주요 평가지표로는 정확도, 정밀도 재현율, F1 점수가 있다.

정확도

  • 정확도(Accuracy)는 실젯값과 예측값이 얼마나 일치되는지를 비율로 나타낸 평가지표이다.

  • 전체 값 중 TP와 TN이 차지하는 비율이 정확도 이다.

\[{TP + TN} \over {TP + FP + FN + TN}\]
  • 평가지표로 정확도를 사용하는 경우는 많지 않다. 10일 중 1일 꼴로 비가 온다고 가정했을 때 매일 비가 안온다고 예측해도 정확도는 90%이다. 높은 정확도가 모델의 우수성을 담보하지 않기 때문에 정확도를 평가지표로 잘 사용하지 않는다.



정밀도 : 객체가 있다고 예측한것 중에 실제로 객체가 있는 경우

  • 정밀도(Precision)는 양성 예측의 정확도를 의미한다. 양성이라고 예측한 값(TP + FP) 중 실제 양성인 값(TP)의 비율이다.
\[TP \over {TP + FP}\]

  • 정밀도는 음성을 양성으로 잘못 판단하면 문제가 발생하는 경우에 사용한다. ex) 스팸 메일 필터링 스팸 메일은 양성, 일반 메일은 음성이라고 할 때, 양성을 음성으로 잘못 판단하면, 즉 스팸을 일반 메일로 잘못 판단하면 받은 메일함에 스팸이 하나 들어올 것이다. 그러면 지우면 그만이지만 음성을 양성으로 잘못 판단하면, 즉 일반 메일을 스팸으로 잘못 판단하면 업무상 중요한 메일을 받지 못할 수 도 있다. 결론적으로 스팸 필터링은 음성을 양성으로 잘못 판단하면 경우에 문제가 될 때 정밀도를 사용한다.

  • 보통 문제가 되는 상태를 양성, 정상인 상태를 음성이라고 한다.



재현율 : 놓지지 않고 탐지한것

  • 재현율(Recall)은 실제 양성 값(TP + FN) 중 양성으로 잘 예측한 값(TP)의 비율이다. 재현율은 민감도 또는 참 양성 비율(TPR)이라고도 한다.
\[TP \over {TP + FN}\]
  • 재현율은 양성을 음성으로 잘못 판단하면 문제가 되는 경우에 사용한다. ex) 암 진단 암(양성)인데 암이 아니라고(음성) 진단하면 큰 문제가 발생한다. 반대로 암이 아닌데(음성) 암이라고(양성) 진단하면 오진이긴 해도 생명에 문제가 되진 않는다.



F1 점수

  • F1 점수는 정밀도와 재현율을 조합한 평가지표이다. 정밀도와 재현율 중 어느 하나에 편중하지 않고 적절히 조합하고 싶을 때 사용한다.

  • F1 점수는 정밀도와 재현율의 조화 평균으로 구한다.

\[F1 = {2 \over {1 \over precision} + {1 \over recall} } = 2 \times { {precision \times recall} \over {precision + recall} }\]

조화평균

  • 주어진 수들의 역수의 평군의 역수. $a_1, a_2, … a_N$ 에 대해 조화평균을 구하면 \(H = {N \over { {1\over{a_1} }+ {1\over{a_2}} + ... + {1\over{a_N} } } }\)



2.2 로그 손실

  • 로그 손실은 분류 문제에서 타겟값을 확률로 예측할 때 기본적으로 사용하는 평가지표이다.
\[logloss = - {1\over N} \Sigma^N_{i=1} \; (y_i \; log\;(\hat{y}_i) + (1-y_i) \; log \; (1-\hat{y}_i))\]

  • 여기서 $y$는 실제 타겟값을, $\hat{y}$ 는 타겟값일 예측 확률을 나타낸다. ex) 이진분류 문제라고 가정할 때, y는 0(음성) 또는 1(양성)이다. $\hat{y}$ 는 타겟값이 1(양성)일 예측확률이다. 0.1, 0.2, 0.99, etc

  • 실제 타겟값이 1, 0, 1 이고, 타겟값이 1일 확률을 0.9, 0.2, 0.7로 예측했다고 할 때,


실제 타겟값양성 타겟 예측 확률개별 로그 손실 계산 수식계산 값
10.9$1\times log(0.9) + (1-1) \times log(1-0.9)$-0.1054
00.2$0 \times log(0.2) + (1 - 0) \times log(1-0.2)$-0.2231
10.7$1 \times log(0.7) + (1-1) \times log(1-0.7)$-0.3567

세 값의 평균에 음의 부호를 취한 값인 0.2284가 최종 로그 손실값이다.



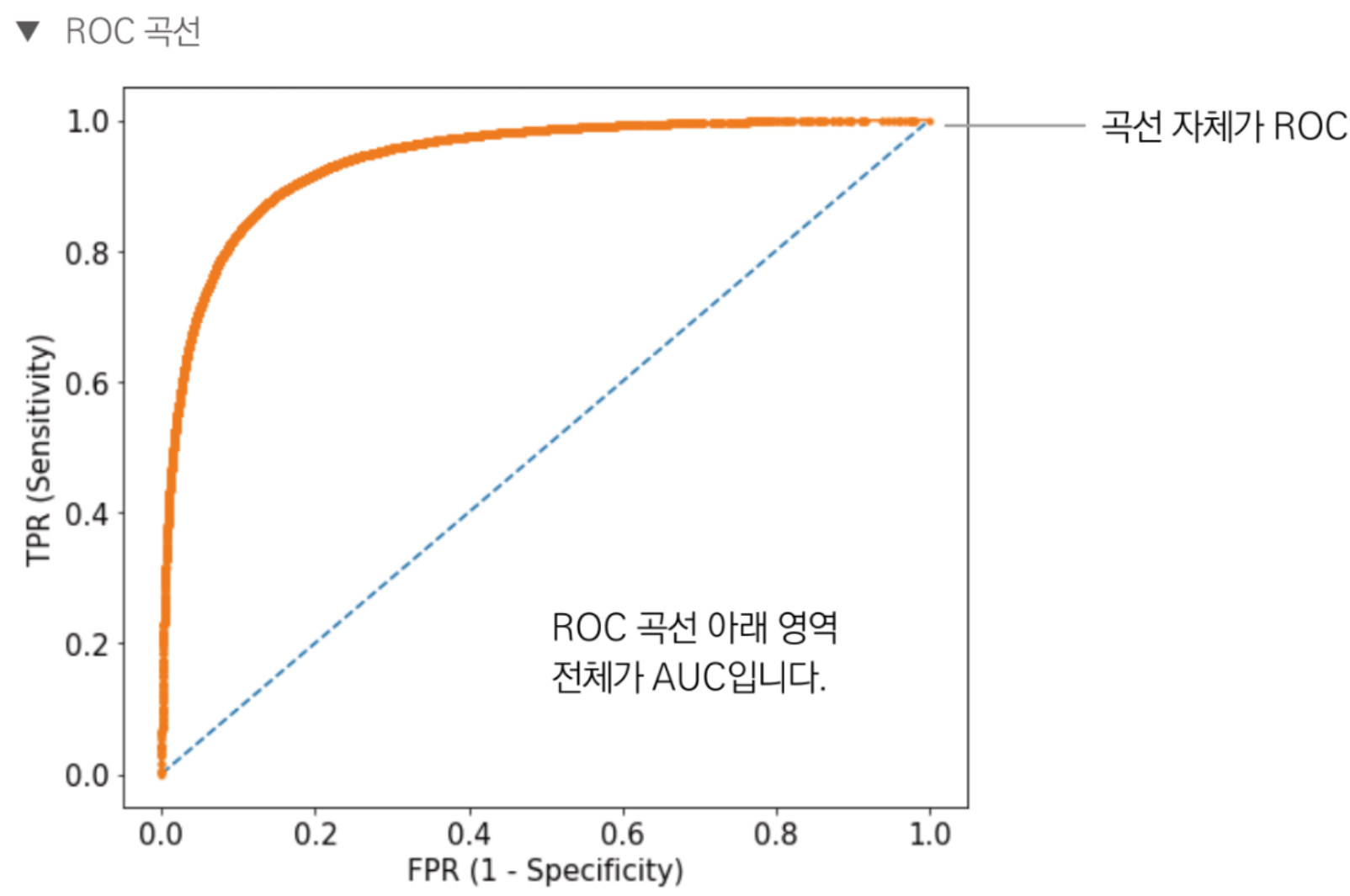
2.3 ROC 곡선과 AUC

  • ROC (Receiver Operating Characterisitc) 곡선은 참 양성 비율(TPR) 에 대한 거짓 양성 비율(FPR) 곡선이다.

  • AUC (Area Under the Curve)는 ROC 곡선 아래 면적을 말한다. AUC는 기본적으로 예측값이 확률인 분류 문제에서 사용한다.

타겟값(이산값) 으로 예측 시 분류 평가 지표 : 정확도, 정밀도, 재현율, F1 점수

타겟 확률로 예측 시 분류 평가지표 : 로그 손실, AUC

  • 참 양성 비율(TPR)은 양성을 얼마나 정확히 예측하는지 나타내는 지표로, 재현율과 같은 개념이다.

  • 참 음성 비율(TNR)은 음성을 얼마나 정확히 예측하는지 나타내는 지표이다. 특이도(specificity)라고 한다. 참 음성 비율(TNR) 수식은 아래와 같다.

\[TN \over {FP + TN}\]
  • 거짓 양성 비율(FPR) 은 1 - 참 음성 비율(TNR) 이다. 즉, 1 - 특이도 이다.
\[FPR = {FP \over {FP + TN}} = 1 - {TN \over {FP + TN}} = 1 - TNR\]
  • TOC 곡선은 참 양성 비율(TPR) 에 대한 거짓 양성 비율 (FPR) 곡선이다. 달리 말하면 민감도 (1 - 특이도) 에 대한 곡선이다.

  • 그림의 가로축이 거짓 양성 비율, 세로축이 참 양성 비율이다. 가운데 점선은 완전 무작위 분류 시 ROC곡선이다. 즉, ROC 곡선은 위쪽으로 멀어질수록 성능이 좋은것.


  • FPR, TPR 모두 0부터 1 사이의 값을 갖는다. 또한 AUC는 곡선 아래 면적을 의미하기 때문에 100%완벽하게 분류하면 AUC가 1이고, 완전 무작위로 분류하면 0.5이다. 다시 말해 모델 성능이 좋을수록 AUC가 크다.

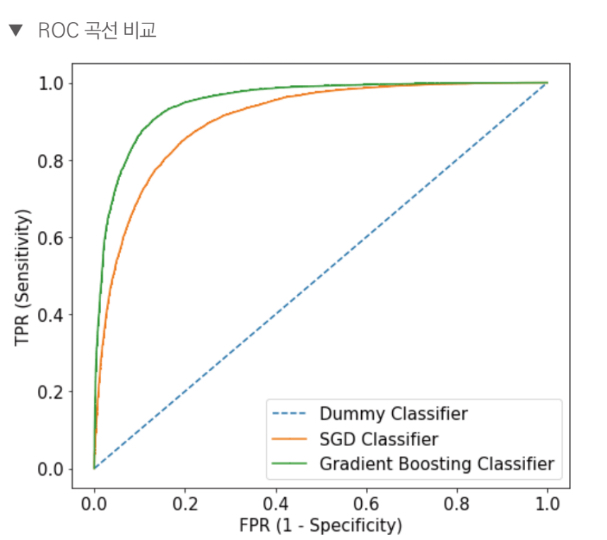
  • Gradient Boosting의 ROC곡선이 SGD의 ROC곡선보다 위에 있으므로 Gradient Boosting의 AUC가 더 크고 성능이 더 우수하다고 할 수 있다.
Machine Learning, Part2
Machine Learning 이론 개념
This post is licensed under CC BY 4.0 by the author.